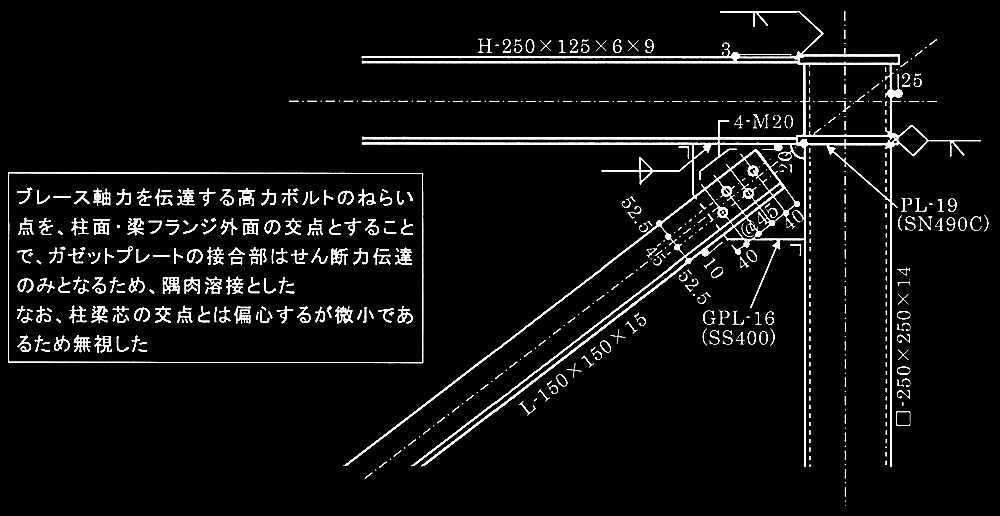
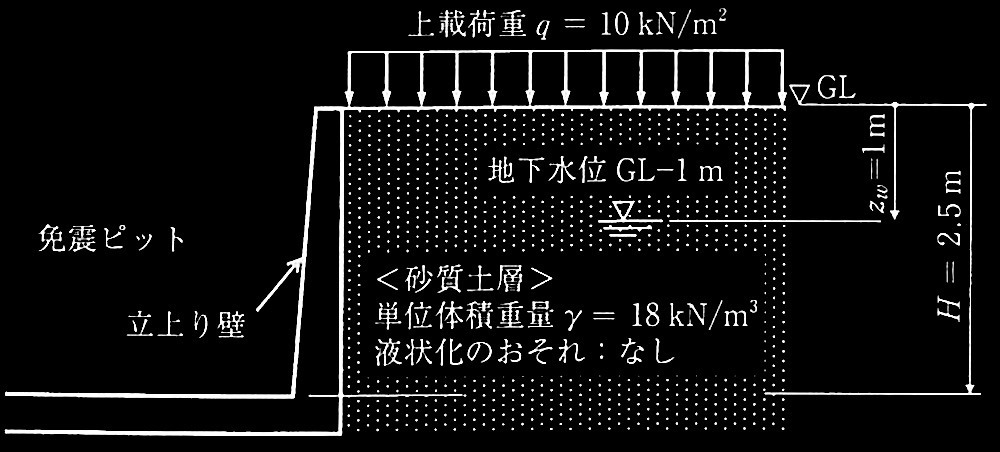
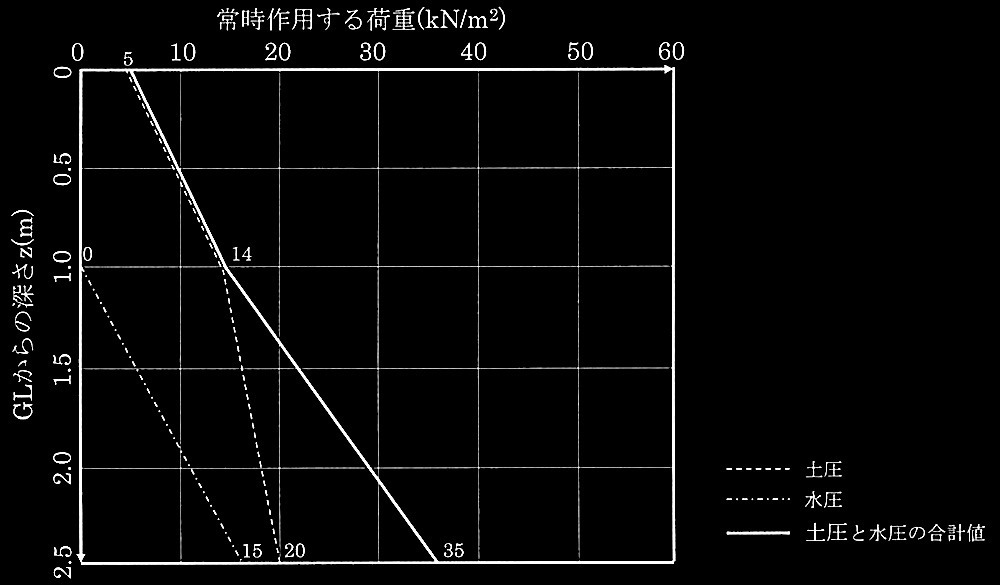
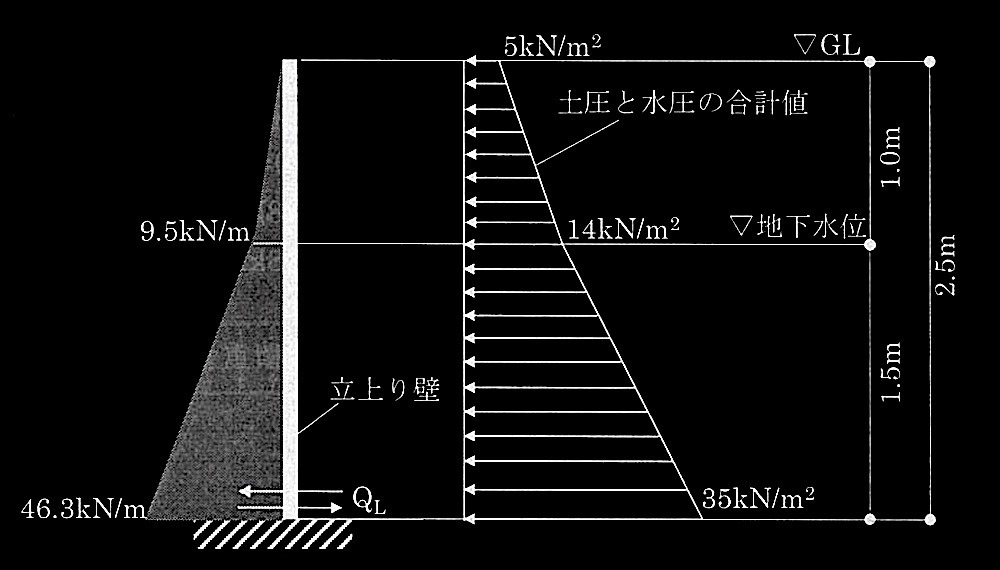
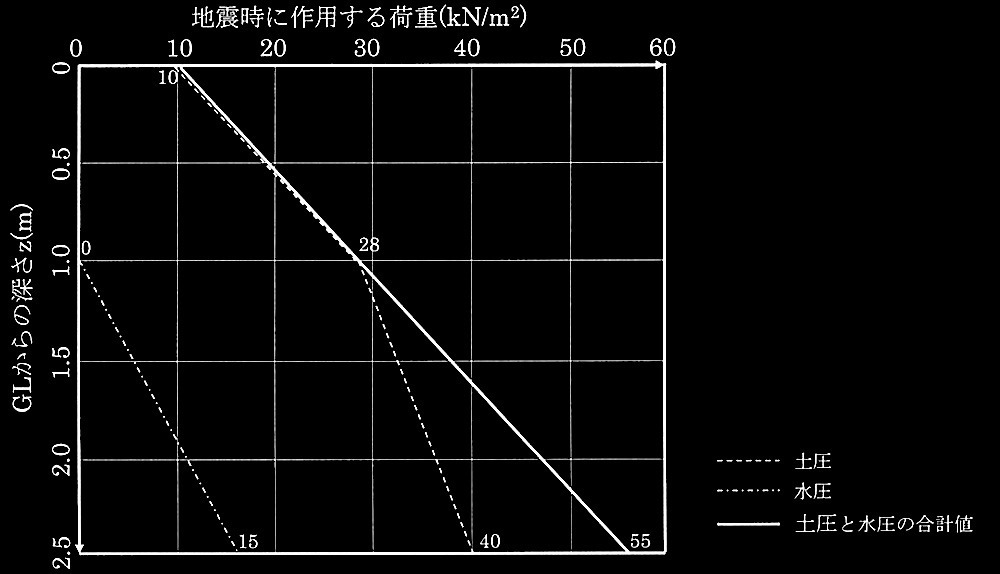
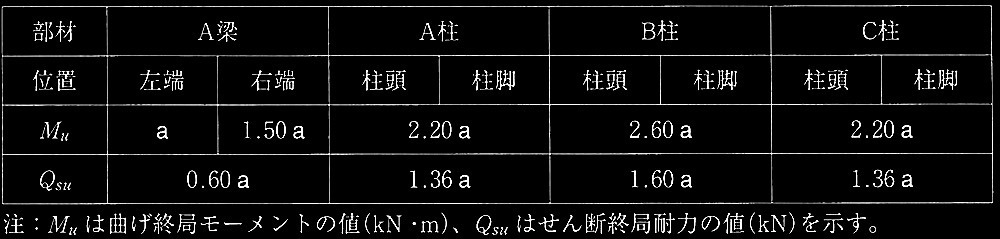
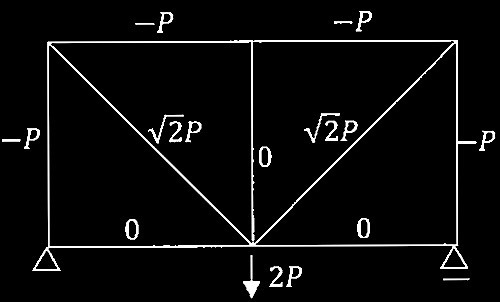
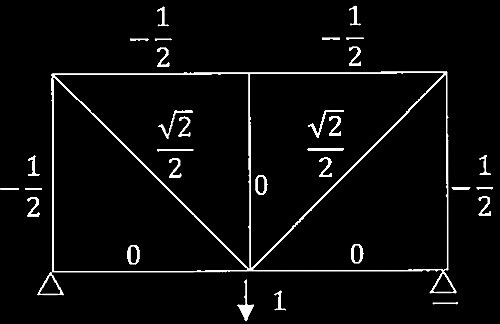
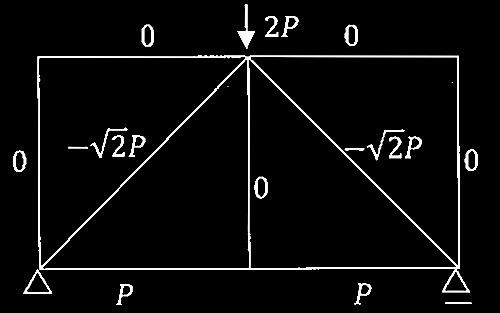
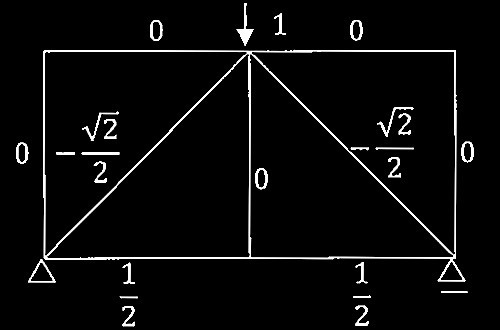
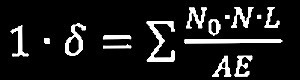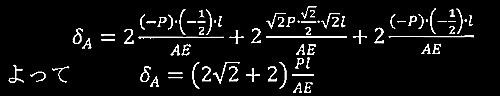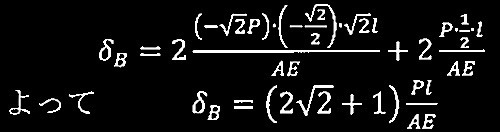問題1
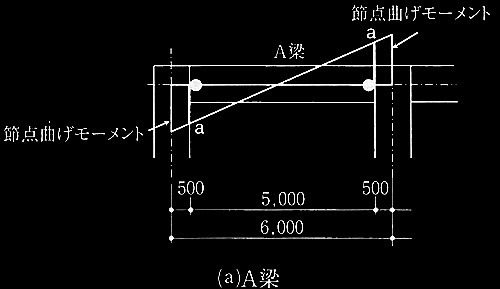
図1(a)に示す、長方形断面をもつ鉄筋コンクリート造柱が、断面重心位置に作用する一定軸力N(圧縮を正とする)の下で終局曲げモーメントM u に達する場合を考える。終局曲げモーメントM u は、図1 (b)のひずみ分布に示すように、コンクリート圧縮縁ひずみが終局ひずみ ε cu に達したときの断面重心回りのモーメントとする。ひずみ分布として軸力の大きさに応じた典型的な分布 i 〜ivを考え、これらのひずみ分布間の領域を、それぞれ領域 (A)〜(E)とする。断面には平面保持の仮定が成立し、コンクリートは引張応力を負担しないものとする。圧縮コンクリートの応力は、図2に示す等価圧縮応力ブロックを用いる。なお、鉄筋の応カーひずみ関係は完全弾塑性のバイリニア形とする。図3に、断面のN-M u 相互作用図を示す。図中にはひずみ分布 i 〜iv、及びその間の領域(A)〜(E)を示す。
以下の[ No.1 ]〜[ No.3 ]の設問に解答せよ。
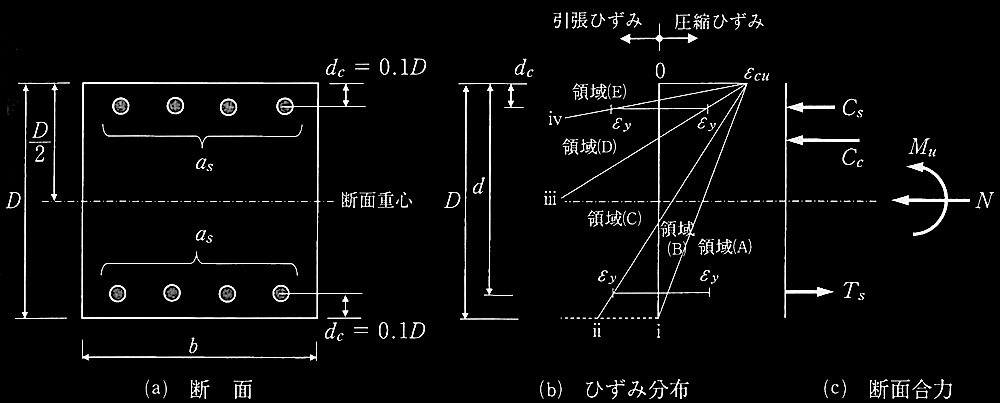
図1 一定軸力の下で曲げ終局状態に達する柱
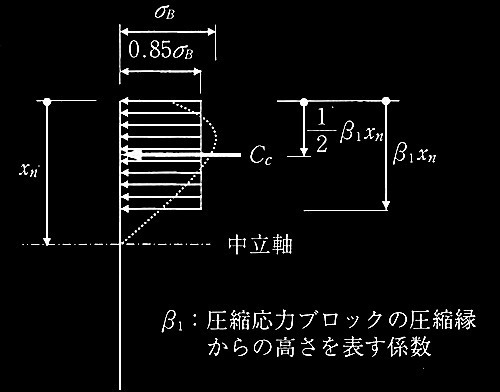
図2 コンクリートの等価圧縮応カブロック
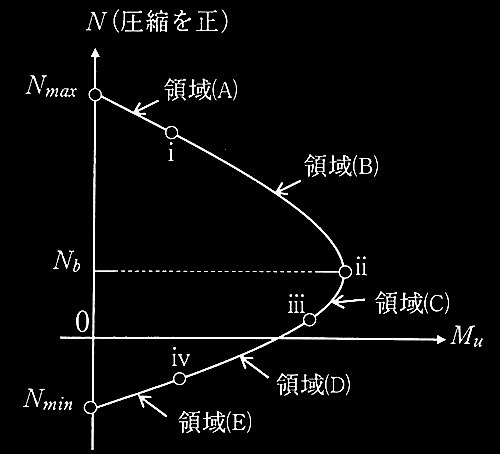
図3 断面のN-Mu相互作用図
【記号一覧】
b:柱断面の幅
D:柱断面の全せい
a s :圧縮鉄筋、引張鉄筋それぞれの断面積
d c :圧縮縁または引張縁から圧縮鉄筋または引張鉄筋中心までの距離で d c = 0.1D
d:圧縮縁から引張鉄筋中心までの距離(有効せい)d = 0.9D
σ B :コンクリートの圧縮強度
σ y :鉄筋の降伏点
ε cu :コンクリートの曲げ圧縮縁ひずみ
ε y :鉄筋の降伏ひずみ
C c :コンクリートの圧縮合力(圧縮を正)
C s :圧縮鉄筋の圧縮合力(圧縮を正)
T s :引張鉄筋の引張合力(引張を正)
x n :圧縮縁から中立軸までの距離(中立軸深さ)
[ No.1 ]
下記の?@〜?Dの状態は、それぞれ図l(b)及び図3で表した領域(A)〜領域(E)のどの領域に相当するかを選び、解答欄に領域の記号(A〜E)を記入せよ。
?@ 引張鉄筋も圧縮鉄筋も引張降伏している状態。
?A 引張鉄筋は引張降伏していて、圧縮鉄筋は圧縮降伏している状態。
?B 引張鉄筋は引張降伏していて、圧縮鉄筋は弾性範囲の状態。
?C 全断面が圧縮の状態。中立軸は断面外にあり圧縮応カブロックは適用できない。
?D 引張鉄筋は弾性範囲で、圧縮鉄筋は圧縮降伏している状態。
答え
[ 解答解説 ]
?@引張鉄筋も圧縮鉄筋も引張降伏(引張領域)にあることから、 領域E
?A引張鉄筋はε y
に到達し、圧縮鉄筋もε y
に到達することから、 領域C
?B引張鉄筋はε y
に到達するが、圧縮鉄筋は弾性範囲でε y
に到達しないので、 領域D
?C全断面が圧縮領域なので、 領域A
?D引張鉄筋は弾性範囲でε y
に至らず、圧縮鉄筋がε y
に到達することから、 領域B
[ No.2 ]
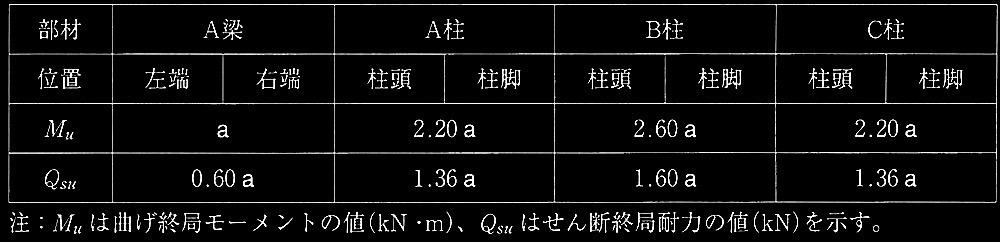
軸力が図3の軸力Nb(圧縮を正)のとき、終局曲げモーメントMuを求める以下の記述につ いて、空欄?@〜?Iに入る適切な式または用語を、この設問末尾の選択肢(あ)〜(ひ)の中から選んで、解答欄にその記号(ひらがな)を記入せよ。ただし、同じ記号を複数回選択してもよい。
軸力がNbのとき、ひずみ分布は (ii)となる。各合力の大きさは、Cc = [ ?@ ]、Cs = [ ?A ]、Ts= [ ?B ]である。ひずみ分布が与えられているので、中立軸深さx n は幾何学的に求めることができる。
x n をε cu 、ε y 及びdで表すと、x n = [ ?C ]となる。軸力Nbは、この x n を用いて、下記の軸方向カの釣合い式から求めることができる。
N b = C s − T s + C c
= [ ?D ]となる。
断面重心に関するM u は、以下のように求めることができる。
M u = C s ・(D/2 − d c ) + T s • (d − D/2) + C c •(D/2 − β 1 x n /2)
= [ ?E ] + C c •(D/2 − β 1 x n /2)
ここで、C c •(D/2 − β 1 x n /2)はN b を含む式として[ ?F ] で表される。
得られた終局曲げモーメントは、?Eが鉄筋による曲げ抵抗、?Fが軸力による曲げ抵抗を表している。
軸力Nbは柱断面の曲げ破壊性状を左右する軸力で、[ ?G ]と呼ばれている。
軸力がN b より大きい場合は、[ ?H ] の [ ?I ] 現象が起らなくなる。

答え
[ 解答解説 ]
?@コンクリートの圧縮力
C c
= 0.85σ B
× β 1
x n
× b = 0.85β 1
σ B
bx n
・・・(い)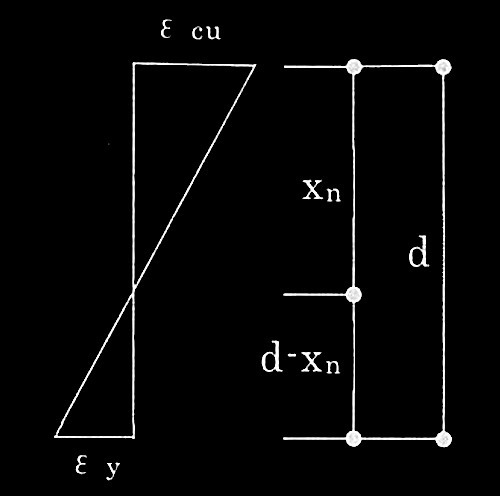
?A 圧縮鉄筋の合力
C s
= a s
σ y
・・・(か)
?B引張鉄筋の合力
T s
= a s
σ y
・・・(か)
?C 中立軸深さx n
ε cu
: ε y
= x n
: d – x n
より、
ε y
•x n
= ε cu
•(d – x n
)
(ε cu
+ ε y
)•x n
= ε cu
•d
x n
= ε cu
/(ε cu
+ ε y
)•d・・・(け)
?D N b
= C s
– T s
+ C c
= 0.85β 1
σ B
bx n
= 0.85β 1
σ B
b•ε cu
/(ε cu
+ ε y
)•d・・・(さ)
(∵ T s
= C c
= a s
σ y
)
?E C s
•(D/2 – d c
) +T s
• (d – D/2) = a s
σ y
• (D/2 – d c
+ d – D/2) = a s
σ y
• (d – d c
)
= 0.8a s
σ y
D・・・(そ)
( ∵ d = D – d c
よりd – d c
= D – 2d c
= 0.8D)
?F ?DよりC s
= T s
からN b
= C c
なので、
N b
•(D/2 – β 1
x n
/2) = N b
/2・(D –β 1
•N b
/0.85β 1
σ B
b)
= N b
D/2•(1 – N b
/0.85σ B
bD)・・・(た)
?G 軸力N b
は、 (と)釣合軸力と呼ばれる。
?H,?I 軸力がN b
より大きい場合は、断面の圧縮性状が支配的となり、 (ね)引張鉄筋の (は)引張降伏現象が起こらなくなる。
[ No.3 ]
図4は同断面で、軸力比(作用軸力の断面圧縮耐力に対する比)のみが異なる鉄筋コンクリート造柱の断面のモーメントと曲率の関係を表している。通常の軸力の範囲であれば、軸力比が大きい場合は、最大モーメントは大きくなり、限界変形(抵抗モーメントが最大モーメントから95%に低下したときの変形)は小さくなる。その理由をそれぞれ記述せよ。
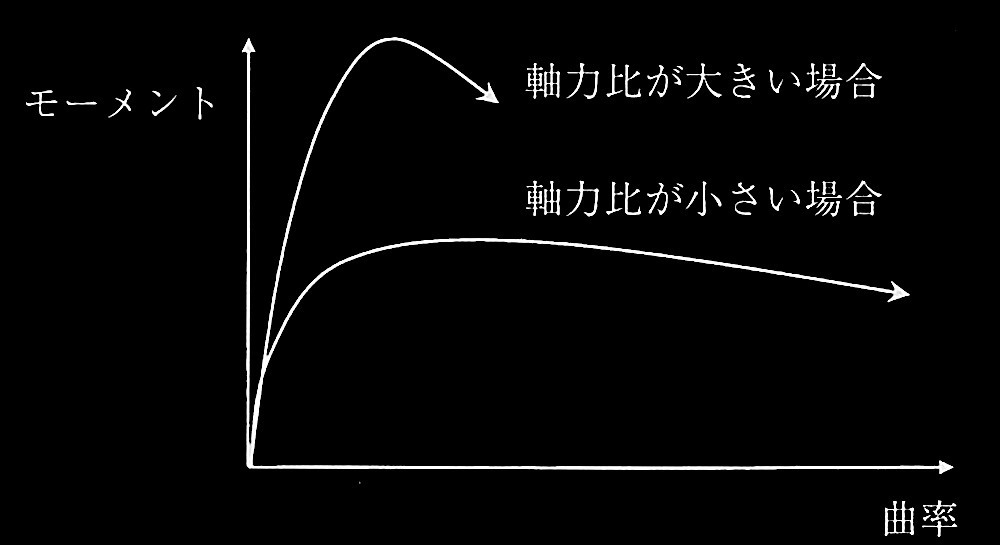
図4 柱断面のモーメントと曲率の関係
答え
曲率が同じRC柱断面において、軸力比が大きい場合は、コンクリートの負担する圧縮合力の割合が大きくなる。その結果、最大モーメントは大きくなる。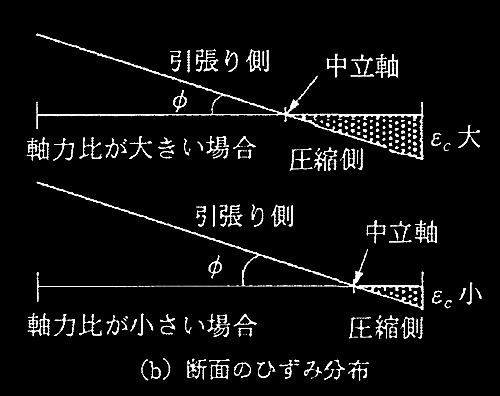
一方、圧縮縁から中立軸位置までの距離が長く、圧縮縁近傍における圧縮ひずみも大きくなる。よって、コンクリートの最大耐力以後の耐力低下の影響が変形の早い段階で顕著になるため、限界変形は小さくなる。