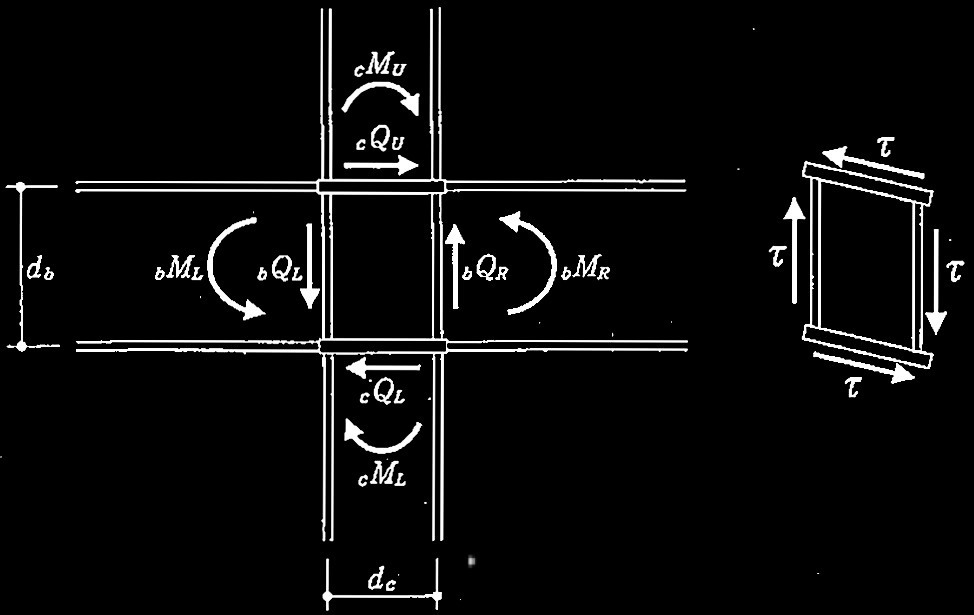
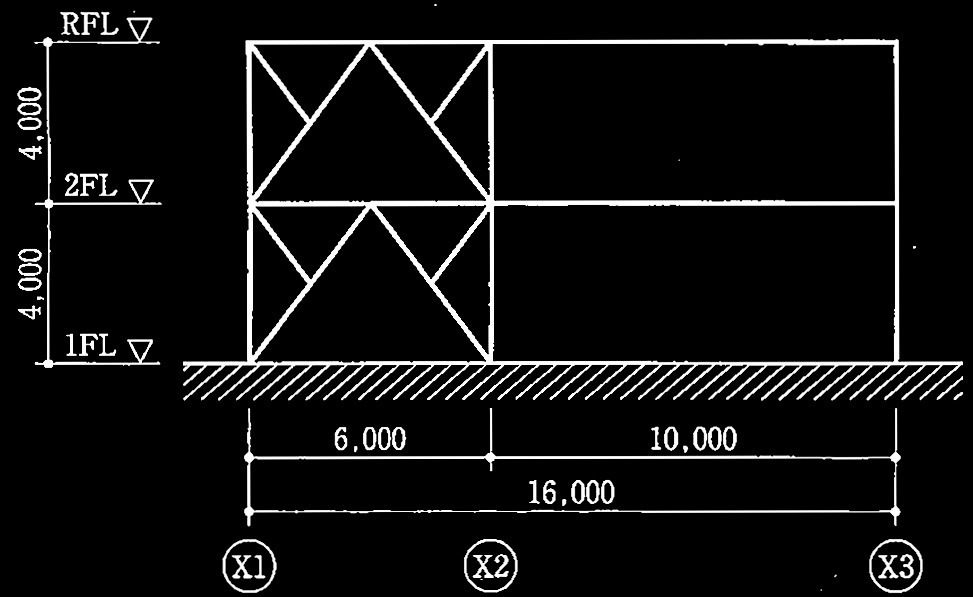
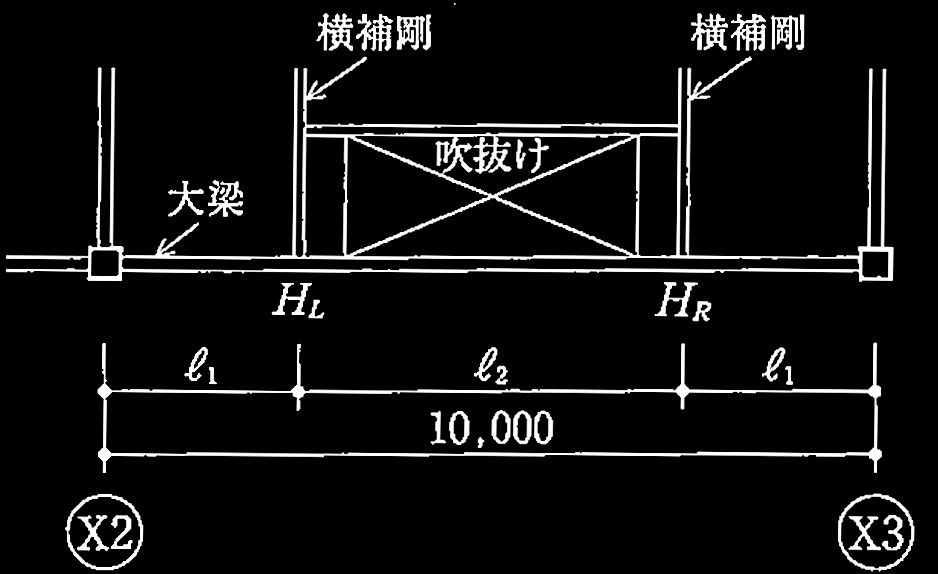
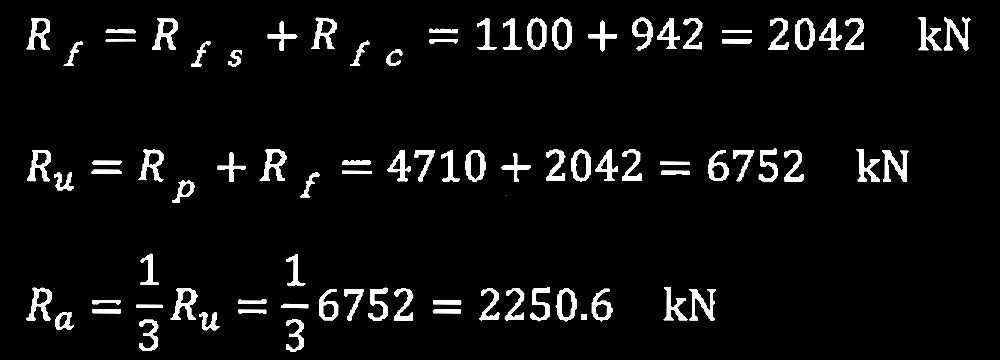問題3
次の「直接基礎(独立フーチング基礎)の設計に関する設問」及び「杭基礎の鉛直支持力等に関する設問」について解答せよ。
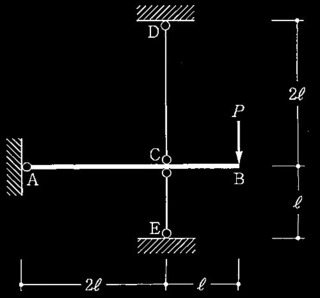
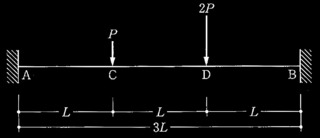
[ No.1 ]
次に示す建築物の基礎を、硬質粘性土地盤を支持層とする直接基礎(独立フーチング基礎)で設計する場合の、長期接地圧及び即時沈下量の検討に関する次の?@〜?Bの設問について解答せよ。
く建築物概要>
・階 数:地上3階建て(地階なし)
・構造種別:鉄筋コンクリート造
く検討の対象とする独立フーチング基礎の概要>
・長期鉛直荷重:W= 1,000kN(フーチング自重含む。)
・底版形状 :正方形(2m × 2m)、根入れなし
く支持地盤の概要 地盤係数等>
・土 質 :粘性土
・粘着カ :c = 150 kN/m 2
・地盤のヤング係数:Es = 20,000 kN/m 2
・支持力係数:N c = 5.1
?@ 地盤の長期許容鉛直支持力度 q α を式(1)により求め、検討の対象とする独立フーチング基礎の長期接地圧 q(基礎底版に作用する単位面積当たりの荷重)との比較により、支持地盤の安全性を検証せよ。ただし、αは形状係数であり、表による。
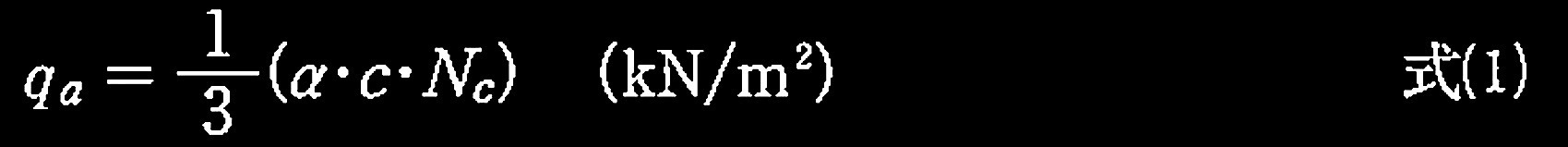
表 基礎形状と形状係数

?A 検討の対象とする独立フーチング基礎の即時沈下量S E を式(2) により求め、独立フーチング基礎の沈下に対する安全性を検証せよ。ただし、本建築物の即時沈下の総沈下量の限界値は20mmとする。

?B ?@及び?Aの結果に関わらず、即時沈下量S E が総沈下量の限界値 20mmを超えた場合には、構造設計者として、どのような対処をすればよいかを簡潔に記述せよ。
答え
[ 解答 ]
?@: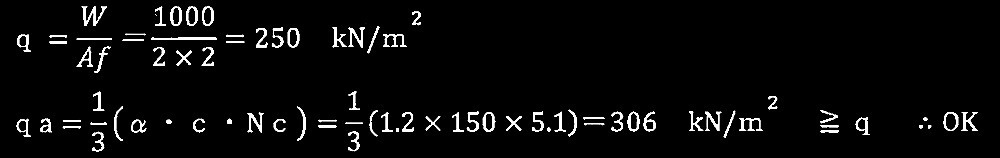
?A: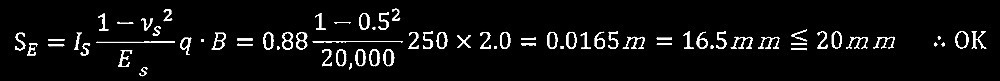
?B:
建物周囲の状況を考慮しつつ、基礎底面積を拡大する。もしくは建物重量を軽くして長期接地圧を低減し、沈下量を抑える。
[ No.2 ]
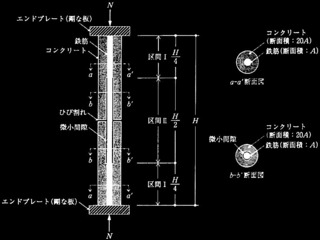
図のような地盤に、直径1mの場所打ちコンクリート杭をGLからGL−21 mまで造成する場合の、杭の鉛直支持力等に関する次の?@〜?Dの設問について解答せよ。ただし、場所打ちコンクリート杭の極限支持力等に関する算定式は、式(3)〜式(7)を用いるものとする。

図 地盤柱状図(概要)
場所打ちコンクリート杭の極限鉛直支持力Ruは、式(3)で与えられる。

?@ 杭の極限先端支持力 R p を求めよ。ただし、杭先端の平均 N 値は40とする。
?A 当該地盤において、液状化の検討を要する層を全て挙げよ。
?B 液状化判定の結果、GL-10mより浅い細砂層及びシルト混り細砂層は、液状化の可能性があることが判明した。その結果を考慮して、当該地盤における砂層の極限周面摩擦力 R fs を求めよ。ただし、杭先端の支持層(砂礫層)への根入れ部の摩擦は考慮しないものとする。
?C 当該地盤における粘土層の極限周面摩擦力R fc を求めよ。
?D 杭の長期許容鉛直支持力R α を求めよ。ただし、杭の自重は考慮しないものとする。
答え
[ 解答 ]
?@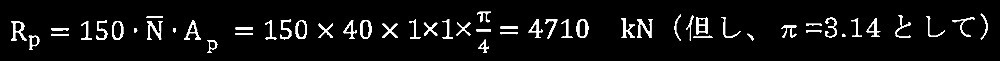
?A
上層より細砂層、シルト混り細砂層、シルト質細砂層。
?B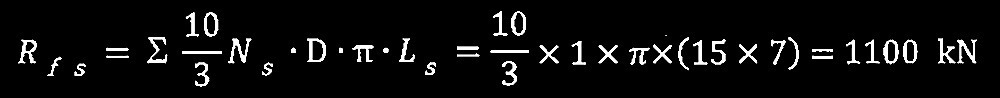
?C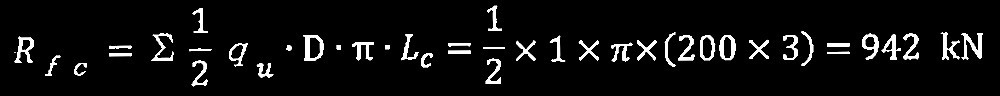
?D