60ばーばの手習い帳

鷗外の『雁』で、雁を外套に隠して持ち帰る場面があります。交番の前を通るとき、さりげなさを粧って、石原が「円錐の体積の求め方」を知っているかと連れのふたりに話を振ります。

　考えてみれば、円錐の体積を求める公式は知っていますが、1/3の意味が今ひとつわかりません。角柱、角錐、円錐の体積について見てみました。
　YouTubeの「環耀」さんのチャンネルがわかりやすかったので、参考にさせていただきました。

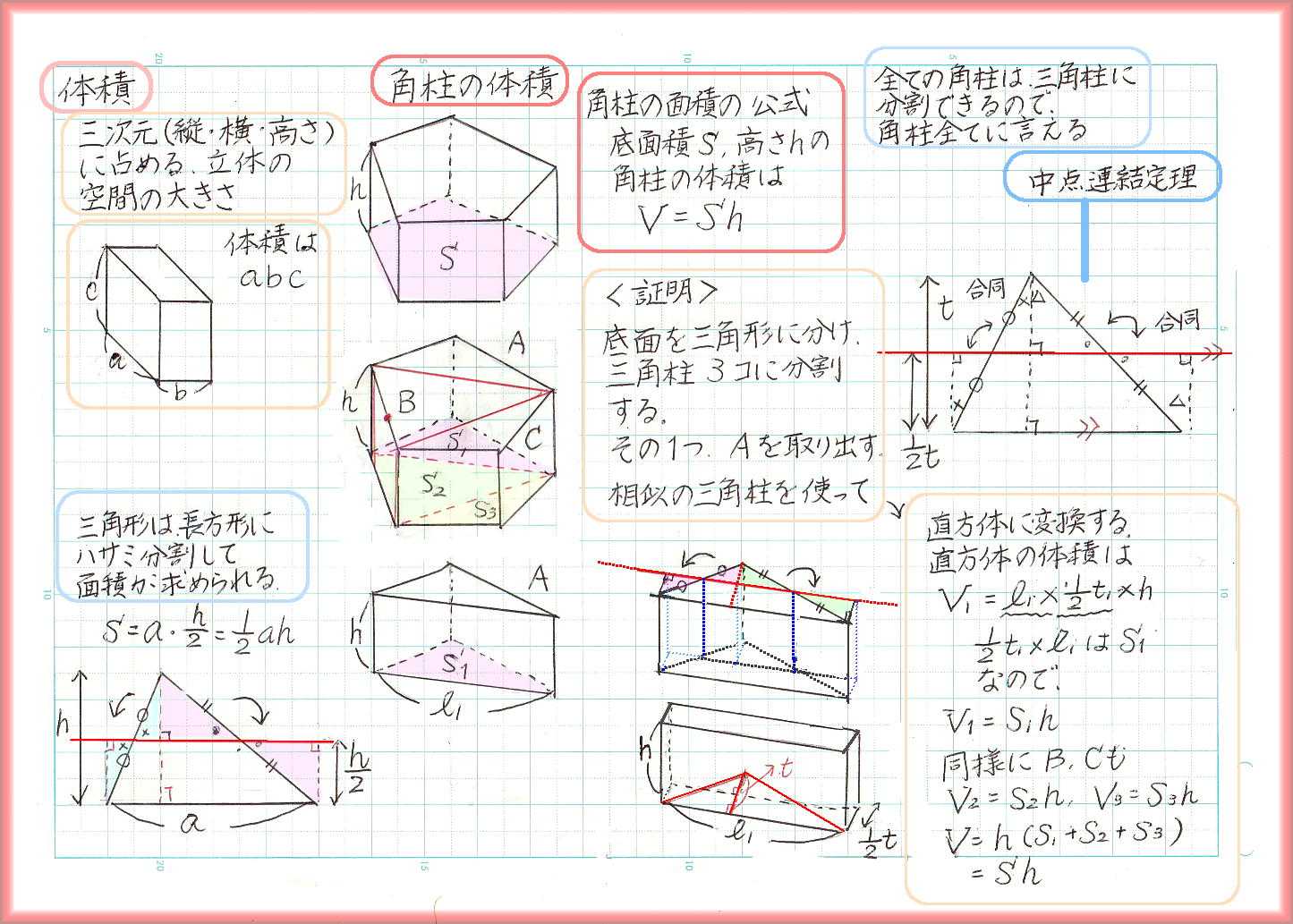
三角形の面積を求めるとき、合同な三角形を2個組み合わせて四角形を作るか、または三角形を切り貼りして四角形に変形させて、面積を求めることをしました。全ての三角形ははさみで切り、位置を移動することで、長方形（正方形含む）に変形することができます。

　同様に、三角柱は、切り取って移動という手段で直方体（立方体含む）に変形でき、そこから三角柱の体積が計算できます。

　全ての角柱は三角柱に分割できるので、三角柱の体積がわかれば、角柱全般の体積がわかります。こうして、V＝Sｈ（体積は底面積×高さ）という小学校で習う角柱の体積公式が証明されます。


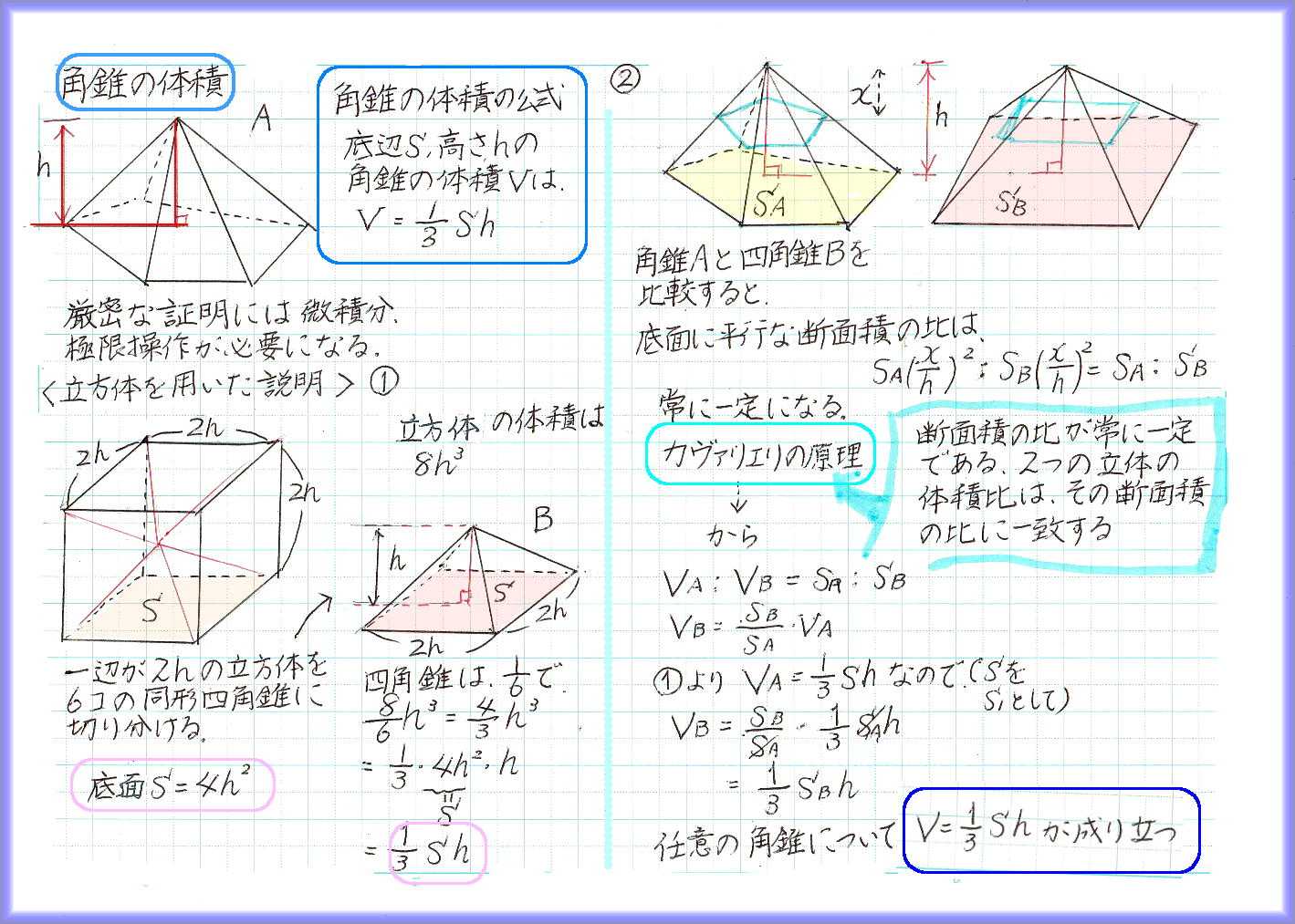
　次に角錐の体積を考えます。残念ながら、角錐の場合は中学校数学の範囲では公式の証明ができません。厳密には微積分の考えを使います。

　小・中学生にもわかる範囲では、立方体を6等分して四角錐を作り、その特殊なケースの体積が底面積×高さの3分の1であることを示すことが多いのです。
　次に「断面積の比が常に一定である立体の体積の比は、その断面積の比に一致する」という原理を用いて、ほかの角錐、円錐の体積も、底面積×高さ×1/3だというように導きます。
　もっと簡単に「立体の体積は底面積と高さによって決まる」とすることもあります。

　カヴァルエリの原理は積分以前に提唱されていました。現代では、微積分の裏付けがあって成立しています。

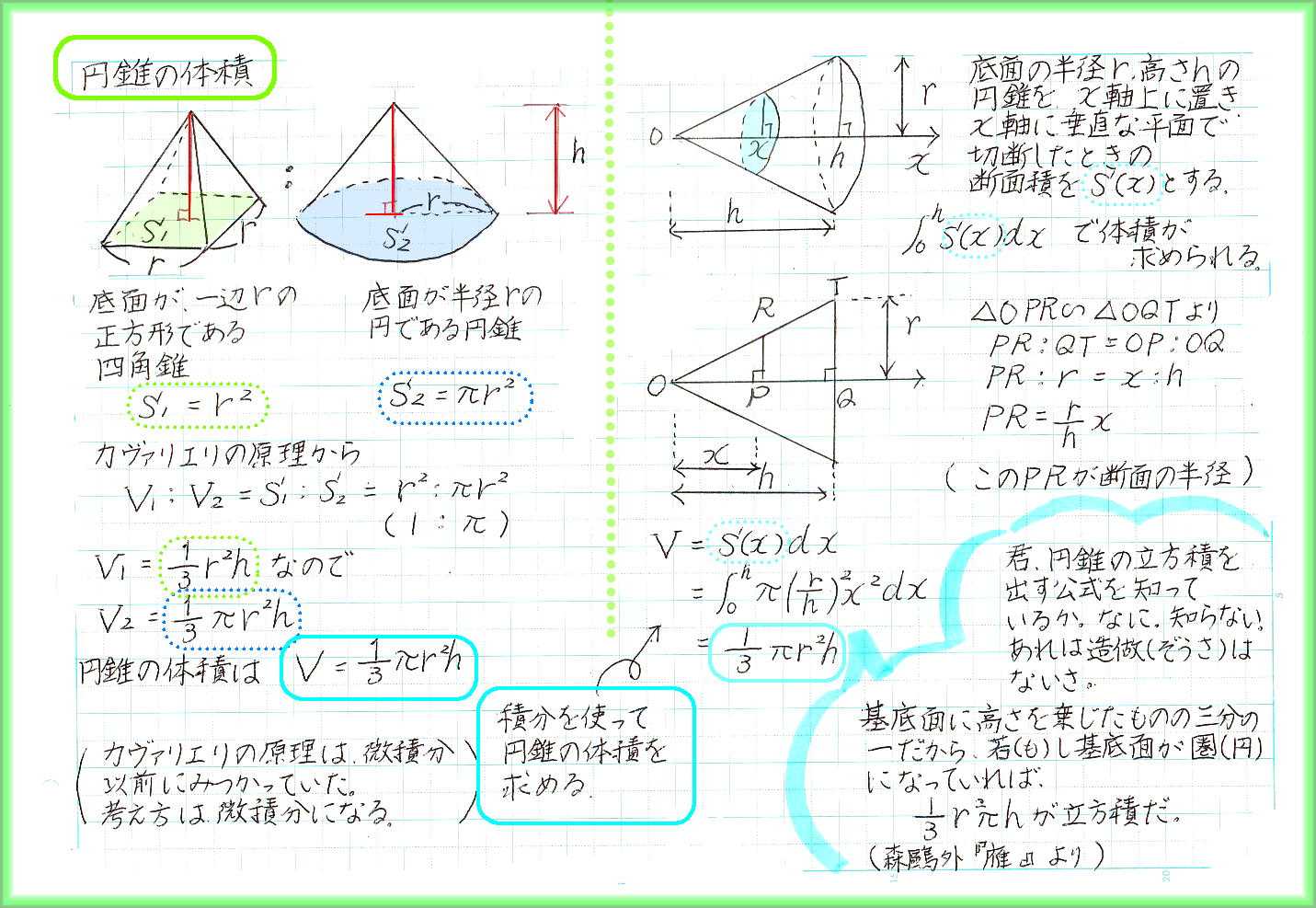
　円錐の体積は、カヴァリエリの原理を認めてしまって、高さの等しい角錐との底面積の比から算出する方法と、積分を使って算出する方法があります。

　高さが微小な円柱を、大きさを変えて底面から頂点まで積み上げたものが円錐だと考えます。π・（r/h）の2乗・ｘの2乗を積分するので、ｘの3乗に係数の1/3が出てきます。
　YouTubeの、鈴木貫太郎さんの動画からわかりやすく教えていただきました。

　ちなみに、円柱だとπ・ｒの2乗を０からｈまで積分するだけでｘの項がないため1/3の係数も現れません。

　さらに、直角三角形を軸の周りに回転させた回転体が円錐であると見て、積分する方法もありますが、私の頭が回転しないのでパスさせていただきます。

　同じ高さ、底面積の円柱と比べて、円錐なら大体3個分か～と目分量でしか理解してこなかった1/3の謎が解けました。

​​​ ​​