全189件 (189件中 1-50件目)
-
にわとりの足は6本
小学校2年生のK君にかけざんを教えていたときのこと。かけざんは、たしざんとは違うけいさんということで、2×3は2+2+2のことではなくて、1当たり量のいくつ分で全体量を求めるけいさんのことだよということで、1当たり量を探そうとしていたときのこと。1当たり量をいろいろ出してもらっているうちに、1当たり量が9のものというところでは、「野球1チーム当たり選手が9人」などという例を考えていた私は、K君の「ロケットのエンジンが1台あたり9つ」という予想をこえた答えに、びっくりし、感心したりしました。それからK君は、エンジンが9つついているロケットの絵を楽しそうに描きました。ところが、1当たり量が2を考えるとき、K君がなかなか答えないので、例えば、「ニワトリ1羽当たり足が2本でしょう」というと、K君は、がぜん違うというのです。「ニワトリの足は、6本だ」というのです。それはつめのところじゃないの?といっても頑固に6本をゆずりません。「2本でしょう」「6本」のやりとりが続きました。K君は物知りで、いろいろなことを知っています。だから、にわとりの足が何本かということで、こんなに見方が分かれるということは本当に意外で、びっくりしてしまいました。その日は、結論を出すことはやめて、1週間ほどたって、もういちどにわとりの足のはなしをすることにしました。ところが、次の週に会ったときにも、まったく同じ展開になったのです。K君は、断固としてにわとりの足は6本だと確信しているのです。私は、ここに教育の面白さのひとつがあると感じました。それから、K君とは会えないでいますが、K君にまた会って、にわとりの話をしてみたいと思っています。
April 16, 2010
コメント(5)
-
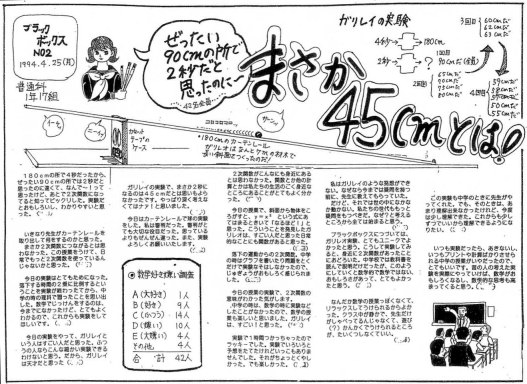
まさか45cmとは!!実験 かけ算わり算から微分積分へ(11)
まさか45cmとは!!落体の実験風景前回の落体の実験風景と授業の感想をまとめた教科新聞{ブラックボックス」(NO2 1994.4.25)発行です。<その1>カーテンレールでどんな斜面を作って転がしたのか、生徒たちの主な感想ータイトルにとりあげたーなどを読み取ってください。<その2>上の教科新聞の右上部分「生徒たちの予想の変化」をピックアップ「生徒たちの予想にもとづいた実験」を4回くりかえしても、「45cm」という答えになかなかならない点を読み取ってください。そこが面白い実験なのですね。<続く>ご訪問有難う御座います。下の2つの教育ブログ・ランキングに参加しています。よろしかったら下のそれぞれのマークをクリックした下さい。ランクの点数が加算されます。人気blogランキングへ
January 22, 2009
コメント(1)
-

カーテンレールの実験 かけ算わり算から微分積分へ(その10)
カーテンレールの実験ガリレオ・ガリレイ(1564~1642)は、落体の法則を発見したことで有名です。この法則は次の2つからなっています。落体の法則>1. 物体が自由落下するときの時間は、落下する物体の質量に依存しない。2. 物体が落下するときに落ちる距離は、落下時間の2乗に比例する。ガリレオが、ピサの斜塔の上から、大小2種類の球を同時に落とし、両方が同時に着地するのを見せたというのは弟子の創作らしいのですが、実際に行なった実験は、斜めに置いたレールの上を、重さが異なり、大きさが同じ球を転がす実験です。斜めに転がる物体ならばゆっくりと落ちるので、これで、重さによって落下速度がかわらないことを実証したのですね。この実験は、その様子を描いた絵画も残っています。当時、中世を支配していたアリストテレスの世界観では、重いものほど早く落下することになっていたので、それがゆらぐということは、天動説そのものがゆらぐ問題になり、アリストテレス派の研究者と論争になったと言われています。ガリレオの斜面は、木製で長さが7mほどあったと言われていますが、私は、高校1年生が二次関数を学び始めるときには、1.8mのカーテンレールに10cmごとに目盛りをつけて、パチンコ玉を転がして、この実験を再現しています。先輩たちのすぐれた実践があり、カーテンレールを4秒で転がる斜面を作ることができるのですね。カーテンレールの上の方から45cmあたりにカセットテープのケースを横に立てるとだいたい4秒で転がる斜面になるのです。1.8mを4秒で転がったとしたら、2秒で転がる距離はどれぐらいかという問題を考え、みんなで予想し、実験で確かめるというものです。生徒たちに質問すると、「2秒で転がる距離は90cm」と答えるのですね。比例感覚に毒されている生徒たちは、時間が半分なら転がる距離も半分であると思い込んでいるのです。だから予想は見事にはずれていくのですね。そこが面白いのです。2次関数を学ぶときに大切なことは、この生徒たちの「常識」をひっくり返すことなのです。そのことは、大学受験のために学ぶなどとは違う、学ぶということの本当の意味や大切さや面白さを学ぶ重要な機会になるからです。生徒たちの既成の考え方を壊したり,ゆさぶったりすることは、授業の原点と考えられます。いきなり公式が出てきて、それに数字をあてはめるだけの数学の授業とは全然ちがうものになりますよね。予想がはずれた生徒たちには、なぜかという疑問が湧いて、二次関数を学ぶ動機と意欲が生まれてくるのですね。ちなみに、2秒で転がる距離はたった45cmにすぎないのです。それが二次関数の特徴なのです。それは、ガリレオが発見したように、落下する距離は、時間に比例するのではなくて、時間の2乗に比例するからです。高校1年でほとんどの生徒が学ぶ「数学1」に出てくる二次関数は、大人になって思い出してみると、ただ「グラフかき」で終わっていて、現在でも、漢字の機械的な反復練習と同様に、いろいろな練習問題で繰り返しグラフをかかせるだけで、なぜ二次関数を学んだのかということは、教師にも生徒にもわかっていないのではないでしょうか。では、この二次関数をどう教えれば面白いのかということを考えたとき、中世の世界観である天動説から、近代の世界観となる地動説へと激動していく時代と結びつけて、ガリレオの実験のもつ意味をとりあげることは大事な出発点になるのではないかと私は考えるのですが、みなさんはどうお考えでしょうか?<続く>ご訪問有難う御座います。下の2つの教育ブログ・ランキングに参加しています。よろしかったら下のそれぞれのマークをクリックした下さい。ランクの点数が加算されます。人気blogランキングへ
January 21, 2009
コメント(1)
-

楽しい関数の授業風景 かけ算わり算から微分積分へ(その9)
楽しい関数の授業風景 これが私のブラックボックスの実物です!!関数について書いてきましたが、授業で具体的にどういうブラックボックスを使ったのかをご覧下さい。教室に持ち込むと、真っ黒で怪しげな大きな物体!!!に生徒も興味津々。まさにこれがブラックな箱!!上の方から「いも」と書いたカードを入れると、なんと!!下の方から「音」と書いたカードが出てくる!!いったい中のしくみはどうなっているのか???授業は、こういうところから始まります。この授業風景を、生徒たちの考えたブラックボックスの作品や授業風景のイラストをまとめて『教科新聞』を一枚発行しました。日付は1990年とあります。新聞の題名は「ひびき」少しは、授業の愉快なフンイキをお届けできたでしょうか???授業では、ブラックボックスを生徒たちが書いているような左側に入口、右側に出口をもつ箱型の図形として表していますが、ブログでは、<○○の働き>と表しています。さて、こういう印象的なブラックボックスを教室に持ち込んだのは、高校数学の中で、-もちろん微分積分の中でもー何度も出てくる関数というものがわからなくなったときに、生徒と教師がここに戻れば、関数とはこういうものだったのかと思い出すことのできる、共有している原点のような役割を果たしてくれるからです。<続く>ご訪問有難う御座います。下の2つの教育ブログ・ランキングに参加しています。よろしかったら下のそれぞれのマークをクリックした下さい。ランクの点数が加算されます。人気blogランキングへ
January 20, 2009
コメント(3)
-

関数とは自動販売機みたいなもの! かけ算わり算から微分積分へ(その8)
関数とは自動販売機みたいなもの! 関数は、自動販売機みたいなものだと言われれば、イメージがもてて、中学で嫌いになった生徒たちも、「なんだ、簡単そうだな」と思えるのではないでしょうか。自動販売機は、入口からお金を入れると、出口からウーロン茶が出てくるというような働きをするものですね。中の働きはわかりませんが、そういう構造をもったものはいろいろあります。こういうものをブラックボックスと呼んでいます。先日、エンジントラブルにあったアメリカの飛行機が、ハドソン川に見事に不時着水したという話しがありましたが、飛行機の墜落事故のときには、このブラックボックスの回収が、原因調査に非常に重要なことはよく知られていることですね。飛行機のブラックボックスは、パイロットの声を入れて、再生するとまたパイロットの声が出てくる働きをするものです。関数の授業に入る時には、いろいろなブラックボックスを紹介しながら、生徒たちにも作品を作ってもらい、関数とは、ある物を他の物に変える働きであるということをつかんでもらうようにしています。例えば、電気 → <電気ストーブの働き> →熱電波 → <携帯の働き> → 声炭酸ガス → <葉っぱの働き> → 酸素勉強の好きな子 → <( ? )> →勉強の嫌いな子 ・・・・・・・・・・・・・・・ というような具合です。みなさんも、何かひとつ愉快な作品を考えてみてはいかがでしょうか。きっと関数がよくわかってきますよ。遠山啓氏は、『数学は変貌する』(国土社)の中で、関数は非常にわかりにくいと書いています。それは、関数というものが、目に見えない“働き”であるからだというのです。だから、普通に学べば、難しくて、嫌いになる生徒たちがたくさん出てくるところなのですね。遠山啓氏は、それを目に見えるようにしてくれたのがブラックボックスだと言っているのですね。ブラックボックスを使うと、急に関数の授業が楽しいものに変わるのですね。ここには、楽しくわかる授業づくりの重要なヒントがありますね。さて、これが数学とどうつながるのか?ということですか、次のブラックボックスを見てください。 1→< ? >→3 2→< ? >→6 3→< ? >→9 4→< ? >→12・ ・・・・・・・・・・・・・・・・・・・・・・・さてこのブラックボックスはどういう働きをしているでしょうか。入ってきた数を3倍する働きということはすぐわかりますね。働きは、英語で function というので、その頭文字をとってf で表すことにすると、入口から入ってくる数を( )で表すと、このブラックボックスの構造は、 f ( ) =3( )と表すことができますから、上のブラックボックスは、 f(1)=3(1)、 f(2)=3(2)、 f(3)=3(3)、 f(4)=3(4)、・・・一般に、x が入ってくると、このブラックボックスは f ( x ) =3( x )と表すことができますね。これが関数の式です。また、このブラックボックスから出てくる数を y で表すと y = 3xとも表すことができますね。だから、同じ関数の表し方は、2種類あるということです。私の関数の授業は、『新・学力への挑戦』(2005)でとりあげております。また、この関数の授業は、1979年の『3年B組金八先生』(脚本 小山内美江子氏)の『数学が好きになる法』で取り上げられました。<続く>ご訪問有難う御座います。下の2つの教育ブログ・ランキングに参加しています。よろしかったら下のそれぞれのマークをクリックした下さい。ランクの点数が加算されます。人気blogランキングへ
January 19, 2009
コメント(3)
-

かけ算わり算から微分積分へ(その7) かけ算から積分へ
かけ算から積分へ 長方形や三角形など直線で囲まれた面積は、かけ算で簡単に求めることができます。多角形の場合も小さな三角形に分割し、その面積を合計することで求めることができます。ここでも、<その1>で取り上げた分析総合という方法が使われています。 これに対して、円の面積は、アルキメデスの場合は、円周率の求め方のところでふれましたように、円に内接する96角形と外接する96角形から、その面積を求めています。 この方法は、当然正多角形の辺数をどんどんふやしていけば、やがて円の面積に限りなく近づくのではないかという考え方と結びついていました。この考え方は、エウドクソス(BC408-355頃)によって唱えられ、「取りつくし法」と呼ばれていますが、積分法の本質を示すものでした。この考え方は、現在の極限の考え方を含んでいて、積分法の入口まで到達していましたが当時、限りなく近づくという無限の考え方を避けようとしたアルキメデスなど有限性を重んじた当時の人たちによって退けられました。 この考え方が息を吹き返したのは、それから1500年もたった16世紀に入ってからでした。プラーエの火星に関する膨大な観測結果を、ケプラーは25年もかけて整理して「ケプラーの三大法則」を発見したのですが、そのひとつが、「太陽と遊星を結ぶ線分は、等しい時間に等しい面積を掃く」というものでした。この法則は、要するに、それまでの円とは異なった曲線(楕円)で囲まれた面積を求める問題になりますから、この面積を求める問題の解決が迫られました。そこで、かけ算に代わる計算方法として、積分法が登場することになるのですが、積分法をつくりあげるためには、デカルトが発見した座標や関数や無限という考え方など近代の数学が新たに発見した道具が必要だったのです。そこで次回は、近代の数学の出発点になった関数について、話をすすめることにします。高校生に数学で嫌いなところをたずねて見ると、図形の証明とともに関数はもっとも嫌いなものになっているからです。何しろ、微分法と積分法は、関数を研究する方法といってもいいわけですから、その関数が嫌いでは大変困るからです。関数大好きになるには???<続く>ご訪問有難う御座います。下の2つの教育ブログ・ランキングに参加しています。よろしかったら下のそれぞれのマークをクリックした下さい。ランクの点数が加算されます。人気blogランキングへ
January 18, 2009
コメント(0)
-

かけ算わり算から微分積分へ(その6) 認識の発展過程に現れる“壁”
認識の発展過程に現れる“壁” 前回、かけ算わり算の壁について書きましたが、このような“壁” は、私たちの良く知っている算数や数学の一番土台になる数の認識の発展過程にも現れてきます。例えば、自然数の壁についてみてみましょう。自然数は、1,2,3,4、・・・ですが、1+2=3のように、自然数を使ったたし算についてはその答えも自然数になるので問題が起きませんが、3-3 や 1-3 を考えると、自然数の世界にない0や負(マイナス)の数が必要になります。自然数はひき算を考えると、自分の世界の中にある数では解決できない壁にぶつかるのです。そこで、この壁を乗り越えるために、自然数に、新たに0や負(マイナス)の数を加えた整数に発展していきます。整数にも壁があります。整数の世界では、たし算やひき算やかけ算は自由にできますが、わり算になるとそうはいきません。答えが整数とならないわり算がいっぱいあるからです。1÷3 などもそのひとつです。この問題を解決するためには、分数というものを数の領域に加えなければなりません。こうして、分数をふくめた数の世界ができます。これが有理数です。ギリシャ時代の数学というとこのあたりまでということになるでしょうか。ピタゴラス学派(教団)は、直角三角形の3辺の間に、ピタゴラスの定理(三平方の定理)が成り立つことを発見したことで有名ですが、無理数の存在を知っていながらそれを否定したことでも有名で、無理数を口外した仲間は簀巻きにして川に放り込まれて殺されてしまったというような逸話もあるほどです。ピタゴラス学派は「万物は数である」という数にかかわる教義をもっていましたが、このときの数は、有理数までだったから、それ以外の無理数などを認めたら、自らの存在そのものを否定することになったからです。皮肉なことに、自分たちで発見したピタゴラスの定理そのものが、じつは無理数を作り出してしまうのですね。1辺が1の正方形の対角線の長さは、√2になりますよね。また、教団のシンボルの五芒星にも無理数が現れてくるのですね。こうして数は、自然数から整数、整数から有理数、さらに有理数の壁を乗り越えて、無理数を含めた実数、実数の壁をのりこえて、2乗してマイナスになる虚数を含めた複素数というようにどんどんその世界を広げて発展していったわけです。かけ算わり算も、その壁を乗り越えて微分積分へと計算の世界を広げていったのです。<続く>ご訪問有難う御座います。下の2つの教育ブログ・ランキングに参加しています。よろしかったら下のそれぞれのマークをクリックした下さい。ランクの点数が加算されます。人気blogランキングへ
January 17, 2009
コメント(0)
-

かけ算わり算から微分積分へ(その5) かけ算・わり算の壁
かけ算・わり算の壁かけ算わり算の壁とは、1当たり量が変化している場合には、使えないという宿命?をもっているのですね。つまりかけ算わり算は、1当たり量が変化していない場合にだけ使える計算法だということです。かけ算わり算には、そこに限界があるのです。例えば、1当たり量の代表的な例として速度があります。物体を高いところから自然に落とせば、その速度はどんどん速くなっていきますね。つまり1当たり量が変化していることになります。この自然落下運動をみたとき、私たちは、小学校の応用問題を解くように、その距離をかけ算で求めようとか、わり算を使って速度を出そうなどとは考えませんよね。最初からあきらめているのですね。それは、大変身の程をわきまえた冷静な態度?だと思うのです。なぜなら、かけ算で全体量を求めるとか、わり算で1当たり量を求めるというのは、じつは、1当たり量が変化していない、つまり、毎時180kmで一定の速さで新幹線が走るとか、毎時4kmという一定の速さで人間が歩くとかいう場合にしか使えないのです。このように見てくると、小学校段階で1当たり量を印象的に学ぶことの重要性が明らかになってきます。いや、高校生や大人たちも、1当たり量などということはちゃんと学んでいないわけですから、改めて学び直すことがとても大切だと言えるかもしれませんね。ところで、この自然落下運動は、誰が見ても、一定の時間には、ある距離を落下しているし、瞬間瞬間である速度をもっているということは紛れもない事実です。 では、その移動した距離やある瞬間の速度をどうしたら求めることができるのでしょうか?これは大変難しい問題です。人間が近代になってぶつかった非常に大きな難問だと思うのです。この人間につきつけられた難問は、かけ算わり算では解決できない壁でした。それをどうやって乗り越えたらいいのか、そのヒントをデカルトが与えてくれたのですね。それが分析総合という方法を使うということでした。<続く>ご訪問有難う御座います。下の2つの教育ブログ・ランキングに参加しています。よろしかったら下のそれぞれのマークをクリックした下さい。ランクの点数が加算されます。人気blogランキングへ
January 13, 2009
コメント(0)
-

かけ算わり算から微分積分へ(その4) 掛け算は「同じ数を何回も加える加法の簡潔な表現」か?
かけ算は「同じ数を何回も加える加法」と考えてもよいのでしょうか?みなさんは、かけ算を学んだ記憶の中に、1当たり量ということを学んだ記憶はあるでしょうか?かけ算といえば、九九について、「放課後まで残されて覚えさせられた」とかいうような記憶はいろいろ聞くのですが・・・。微分積分に関係の深い量として、1当たり量と全体量があり、それが、じつは、小学校2年で学ぶかけ算の中に出てくる量のとらえ方なのですね。このことは、かけ算をどのように教えるのかという点で、昔から文部省(現在の文部科学省)が学習指導要領で示した教え方に重大な問題点があったからではないかと私は考えています。そのかけ算の教え方は、小学2年の段階では、まだ問題がおきないのですが、分数のかけ算やわり算が出てくるとたちまち行き詰まる考え方なのです。そして重要なことは、その後の一次関数のグラフの直線の傾きや、微分で出てくる微分係数などに発展的につながっていく教え方にもなっていないわけです。その最大の問題点は、掛け算は「同じ数を何回も加える加法の簡潔な表現」と規定している点です。つまり、「かけ算というのは、結局、同じ数のたし算なんだよ」と教えなさいと言っていることです。つまり、かけ算というのは、たし算と違う計算法なんですよということを示していないことなのです。このために1当たり量という概念は、出番を失くしてしまうのですね。このことは次の文部省の「乗法」の解説が、昭和53年と平成11年ほとんど同じことを見ても明らかだと思うのです。かけ算はたし算を「簡潔に表現したもの」だと言っているのですね。昭和53年5月 文部省 『小学校指導書 算数編』「乗法は、1つの大きさが決まっているときに、その幾つ分にあたる大きさを求めるという場合に用いられる。つまり、同じ数を何回も加える加法の簡潔な表現として乗法による表現が用いられることになる。」 平成11年5月『小学校学習指導要領解説 算数編』 「乗法は、1つ分の大きさが決まっているときに、その幾つ分かにあたる大きさを求めるという場合に用いられる。つまり、同じ数を何回も加える加法、すなわち累加の簡潔な表現として乗法による表現が用いられることになる。」教科書が、この学習指導要領によって作られ続けているのですから、恐ろしいことです。現在、莫大な費用をかけて「全国学力テスト」などやる前に、文部科学省の「学力」そのものが問われているといえるでしょう。 大切なことは、たし算とは違う量の関係を扱うものとしてかけ算をおさえることなのですね。 たし算は同種の量の関係です。だから、2匹+2匹+2匹=6匹 とその計算には全部同じ種類の『匹』という単位が付きます。 2匹+4本 などという計算はないのですね。かけ算を 2×3=2+2+2 と2を3回たすことだと教えると、分数が出てくると途端にお手上げになります。 2×1/3=?・・・2を何回たすんですか?もう2を1/3回繰り返してたすということでは意味不明になってしまいますね。 これにたいして、かけ算は異種の量の関係を表しているのです。 例えば、アリ1匹当たり足6本で、3匹分では足は全体で18本 という関係を 6本/匹×3匹分=18本と表すのですね。異種の量の関係だから、単位はもちろん全部違うのですね。かけざんとは、1当たり量のいくつ分(いくら分)から全体量を求めることと、はじめからたし算とは違う計算だよということで教えた方が発展的だと思うのです。かけ算をこのように考えたときに、小学校2年で勉強できるのかということを心配される人もいるかもしれませんが、それは、子どもたちにとってはとても楽しくできる勉強なのです。1当たり量や全体量 に晴れの出番が回ってきます。小学校2年生が知っている愉快な1当たり量はいっぱいあるからです。例えば、1当たり量が6のもの・・・トンボ1匹当たり足6本、カブトムシ1匹当たり足6本・・・1当たり量が2のもの・・・ツル1匹当たり足2本、すずめ1匹当たり羽2枚・・・1当たり量が5のもの・・・桜の花1つ当たり花びら5枚、1当たり量が0のもの・・・へび1匹当たり足0本、カエル1匹当たりへそ0個、・・・ 0×3 は、機械的に0と覚えるのではなく、へびの足やカエルのヘソ等を使って、その全体量を求める計算として、0になることを楽しく学ぶこともできるのですね。カエル1匹当たりヘソ0個で3匹分では、ヘソは全体で0個<関連する私の過去のブログもご参照ください>かけざんとは? 6×3は6+6+6のこと?(2005.9.8) マイナス×マイナスはなぜプラス?(2005.9.28) 2年生の掛け算の意味をとりあげた授業を見学(2005.9.29) 次回は、掛け算が行き詰まる場面と分析総合という方法を使ってその壁を乗り越えていくことに話をすすめます。<続く>ご訪問有難う御座います。下の2つの教育ブログ・ランキングに参加しています。よろしかったら下のそれぞれのマークをクリックした下さい。ランクの点数が加算されます。人気blogランキングへ
January 12, 2009
コメント(1)
-
たすけてください!日記が書き込めないのです
日記が書き込めなくなりました!!!タイトルも本文も書き込めないのです。文字を受け付けなくなるのです。キーボードをたたいても、うんともすんともいわなくなるのです。問い合わせをしようにも連絡先も不明!困ってしまいました!原因・解決法 ご存知の方教えてください。メモリーなどに問題があるのでしょうか?ちなみに、デザイン設定を変更すると1回ぐらいは書き込めることがあるのです。ぜんぜん書き込めない場合もありますが・・・今回もデザインを変更したら、書き込めるようになりましたが、多分、次回はだめになると思います。毎回 デザイン設定を変更して、日記を書くことも出来ないし、弱り果てています。どなたか教えてください!
January 12, 2009
コメント(0)
-

かけ算わり算から微分積分へ(その3) 微分積分と分析総合
微分積分と分析総合 ここまで、分析と総合という方法とはどういうことかということを述べてきました。 今日は、この方法を高校数学のひとつである微分と積分についてどのように現れてくるのかを見ていくことにします。 デカルトは「困難は分割せよ」と言い、分割ということはぶつかった困難を小さく分けて考えていくこと、つまり分析することだといいました。また、その細かくわけたものをもう一度系統立てて並べ替えることが総合だと言いました。 じつは、微分積分という計算法は、掛け算割り算を発展させたものなのです。 そういう学び方は現在の高校教科書では示されていませんが、掛け算割り算で解決しようとすると壁にぶつかる、その壁を乗り越える方法として分析総合という方法が使われるのです。このことが分かるだけでも、私は高校で数学を学ぶ意義は大変大きいと思っています。 掛け算でぶつかった壁を総合という方法でのりこえてたどりついたのが積分法であり、割り算でぶつかった壁を分析という方法で乗り越えてたどりついたのが微分法なのです。 つまり、積分法は掛け算を発展させたもの、微分法は割り算を発展させたものなのです。 掛け算 ⇒ 積分法・・・・どちらも全体量を求める 割り算 ⇒ 微分法・・・・どちらも1当たり量を求める だから、掛け算と積分法は、全体量を求める計算としては共通しており、割り算と微分法は、1当たり量を求める計算という点では共通しているのです。 微分積分を学んだという方も、こういう関係は多分知らなかったのではないでしょうか? このことは、私たちの学力というものが、どれだけ本質的なことを学んでいないかということを示すひとつの具体的な事例となります。私は、こういう本質的な角度から「学力問題」は議論してほしいと思っています。 高校の数学2という教科書を開いて見ますと、まず微分法を学び、次にその微分法を利用して積分法を学ぶという構成になっています。教科書で積分法を学ぼうとしたら、まず微分法を学んでおかなければならないということになっています。 では、それ以外の学び方はないのかといいますと、じつはあるのですね。それが、この分析総合という方法を使った学び方です。しかも、この方法でやれば、積分法を微分法より先に学ぶこともできるのです。 この方法は微分積分の本質、つまりその計算法がどういう成り立ち方をしてきたかが大変よくわかるのです。それはちょうど漢字を学ぶときに、機械的に反復練習をして覚えるのではなく、その成り立ちをちゃんと勉強して覚えていくのに似ています。 ですから、それは、本質がわかるという点で、何のために学ぶのかという高校生の問題意識や知的な関心にもこたえることのできる学び方ではないかと私は考えているのです。 さて、ここで出てきた1当たり量や全体量は掛け算や割り算の時に出てくる大変大切な量のとらえ方なのですね。次回は、そういうところに話をすすめます。<続く>ご訪問有難う御座います。下の2つの教育ブログ・ランキングに参加しています。よろしかったら下のそれぞれのマークをクリックした下さい。ランクの点数が加算されます。人気blogランキングへ
January 11, 2009
コメント(1)
-

かけ算わり算から微分積分へ(その2) 算数数学と分析総合
算数数学と分析総合算数数学と分析総合は切っても切れないほど深く関係していると思いますね。算数や数学は、見方を変えると分析と総合という認識方法を繰り返し無意識のうちに学んでいるとみることもできるのではないでしょうか。例えば前回の学習指導要領改定で、公式として扱われなくなり議論を呼び、今回の改訂では復活した台形の面積。台形の面積は、公式を使わなければいきなり求めることができません。こういうときのために、デカルトは「困難は分割せよ」と言ったわけです。つまり、小さく分解(分析)して考えようといったわけです。台形は、2つの三角形に分解できますから、まず、それぞれの三角形の面積を求める。次にそれらをもう一度合計する、つまり総合するこうして台形の面積が分析と総合という方法を使って求められるということです。アルキメデスは、円周率をもとめるために、円周は、円に内接する正6角形の周の長さと、外接する正6角形の周の長さの間にあることを使って、2倍2倍していって正96角形の周の長さを求めて、円の直径で割って、円周率が、223/7(3.140・・・)より大きく22/7(3.142・・・)より小さいことを明らかにしました。これは、今から2000年も前に、今使われている円周率3.14 を正しく求めているということですから、本当にすごいことです。ここでも細かく分けたものを寄せ集めるという分析総合の方法が使われているのですね。このように、分析と総合という考え方は非常に簡単ですが、非常に威力をもっているということができるのですね。これを、ものごとを考えたり発想したりする武器として身につければ、重要な学力を身につけたということになるのではないでしょうか。私は、数学を学ぶときの学力には、反復練習できたえる反射的な計算力とは違うこういう内容を意識的に大切にしていくことが必要だと考えているのです。だから、数学教育の中でも、重要な方法論として高校生が、この分析総合ということばを知り、その具体的な使い方を覚えれば、それは一生活用することのできる学力になっていくのではないかと思います。例えば、政府が国会に提出した予算案などを考えるときはどうでしょうか。いきなりでは難しくてわからないけれども、予算案をまず分析して、中味をー例えば、政党助成金とか軍事費とか米軍への思いやり予算等々を―ひとつひとつ良いか悪いか吟味して、そして総合してみると、消費税を上げたりしなくても、教育や社会保障などをもっと充実していける道筋なども見えてくるかもしれませんね。算数や数学は、役にたたないという声もよくききますが、じつは、空気のありがたさを自覚していないように、算数数学の中で練習してきた分析と総合という重要な認識の方法は、認識の方法として自覚されていないだけで、無意識のうちに日常的に使われていると考えられないでしょうか。<続く>ご訪問有難う御座います。下の2つの教育ブログ・ランキングに参加しています。よろしかったら下のそれぞれのマークをクリックした下さい。ランクの点数が加算されます。人気blogランキングへ
January 3, 2009
コメント(1)
-

かけ算わり算から微分積分へ(その1) デカルトは座標をどのように発見したか
デカルトは座標をどのようにして発見したのか―分析と総合分析と総合 プロ野球の松井選手をどうみるかというときには、例えば、ヒットと打点とホームランという打者としての3つの要素に分解(分析)してひとつひとつ検討します。逆に、昨年の3つの要素が与えられたら、それを総合して昨年の打者としての成績はどうか、何億円で契約更改ができるかというようなことを考える材料にすることができます。 あるいは、ある人の健康状態をみるときに、まず身長、体重、ウエストと分解(分析)して調べ、次に、これらを総合してメタボか、メタボ予備軍かなどということを判定します。 また、漢字の意味を学ぶ時にも、分析と総合を使います。例えば「鳴」という漢字は、「口」と「鳥」に分解(分析)してそれぞれの意味を考え、それらを総合して「鳴」という漢字の成り立ちや意味を理解することができます。 このように、私たちは、日常的に無意識のうちに分析と総合という方法をフルに使ってものごとを認識しているのですね。デカルトと分析・総合 この分析と総合という方法の重要性をいち早く明らかにしたのがデカルトです。デカルトは、1637年、『方法序説』という本を書いていますが、もとのタイトルは、『理性を正しく導き、もろもろの科学における真理を探究するための方法序説』となっています。 デカルトはこの本の中で、難しい問題を研究するにあたっては4つの方法が大切であるとまとめています。その4つの方法を分かりやすく言い換えてみると次のようになります。第一は、自分が明らかに真理だと認めるもの以外は、まずすべてのことを疑ってかかること第二は、検討しようとする難問は、細かく分けて考えるということ第三は、細かく分けたものを、もう一度合理的に(秩序立てて)並べ替えてみるということ第四は、最後に、見落としがないかもう一度全体を見直すということ この第二の方法が分析するということであり、第三の方法が、いったん細かくわけたものを秩序だって並べ替える、つまり総合するということです。座標の発見 デカルトは、ハエが天井を動いているときに、この動きをどうとらえたらいいのかという難問を、この分析と総合という方法を使って考えたのです。 デカルトは、ハエは1つの動いている点と考え、その点は、天井のあるコーナーを原点と考えると、タテとヨコという2つの要素に分解できるということを発見したのです。 逆に、2つの要素(タテ、ヨコ)が与えられれば、その2つの要素を総合すれば、その点がどこにあるのかその位置がわかります。 こうしてデカルトは、今、私たちが使っている座標というものの考え方を発見したのです。 座標の発見は、2つの要素(x、y)の関係を表す関数の発見となります。座標と関数とそのグラフは、変化し運動するものをとらえる新しい数学の世界の扉を開きました。デカルトから近代の数学が始まるといわれるのはこのためです。 ガリレイの地動説が宗教裁判にかけられる時代は、中世の証明を内容とする幾何学(図形)では役にたたなくて、地上の運動や天体の運動をどうとらえるのかということを解決する新しい数学が必要になってきていたのだと考えられます。<続く>ご訪問有難う御座います。下の2つの教育ブログ・ランキングに参加しています。よろしかったら下のそれぞれのマークをクリックした下さい。ランクの点数が加算されます。人気blogランキングへ
January 2, 2009
コメント(1)
-

ブログ再開の年に
新年明けましておめでとうございます。開店休業状態のこのブログでしたが、なんとか今年は、ボツボツ再開していきたいと思っていますのでよろしくお願いします。サンル川写真は、私の大好きな北海道のサンル川の美しい風景です。昨年秋、8年ぶり、2度目の訪問となりましたが、目に焼きついていたこの風景がどこだったか思い出せないでいましたが、ようやくたどりつくことができて、「ここだったのか」と感激したことを思い出します。サンル川は、ヤマメ釣りで有名な川ですが、名寄川となり、やがて天塩川となって日本海に注ぎます。この間、ダムがなく、ヤマメは海に下り、海で大きくなってサクラマスとなって,産卵にもどってくることのできる川です。こんなダムのないすらしい川がまだ日本には残っていたのですね。そのサンル川にダムがつくられようとしているのです。ご訪問有難う御座います。下の2つの教育ブログ・ランキングに参加しています。よろしかったら下のそれぞれのマークをクリックした下さい。ランクの点数が加算されます。人気blogランキングへ
January 1, 2009
コメント(1)
-

桜開花 春爛漫の光が丘公園
桜開花 春爛漫の光が丘公園 3月27日桜の花のもたらすあふれるような春のよろこび!ご訪問有難う御座います。下の2つの教育ブログ・ランキングに参加しています。よろしかったら下のそれぞれのマークをクリックした下さい。ランクの点数が加算されます。人気blogランキングへ
March 27, 2008
コメント(0)
-

なぜ、自殺をくいとめることができなかったのか
東京都板橋区の区立小学校6年の男児(12)が25日、卒業式を終えて帰宅した後、自宅マンションから飛び降り死亡していたことが26日、分かった。 自宅居間のテーブルには、男児が書いたと見られる走り書きが残されていた。B5程度の大きさの紙に「死んでおわびします」と一行だけ走り書きされていたという。 板橋区教育委員会や学校によると、5年生と卒業生が一緒に行う「門出の言葉」で、この男児は全員で学校名を唱和する前に「大好きな学校」という部分を「大嫌いな学校」と大きな声で言い換えて発言。一瞬、静まりかえった場内には、ざわざわと動揺が広がったという。 式終了後、クラスで記念写真を撮る際に校長が「どうしてあんなことを言ったのか?」と聞いたところ、男児は「緊張して間違えた」と説明。少し落ち込んだ様子で、帰宅したという。 27日のテレビでは、事前に、級友に「大嫌い」と言い換えると話していたという報道もある。私がこの報道で気になっていることは、校長の質問のしかたである。「どうしてあんなことを言ったのか」という聞き方には、「門出の言葉」について、何も問題がなく、何ひとつ疑問を感じていないことだ。そもそも今、これだけいじめ・自殺が深刻に起きており、いじめ・自殺があってもそれさえ感知できていない学校・校長の実態が多く見られる。子どもたちは、全員一致して、「大好きな学校」でしめくくって、学校名を全体で唱和できるのだろうか。もしそうでないとしたら、「門出の言葉」には、問題がなかったとはいえないのではないか。子どもたちに心にもない言葉を言わせることになったことも考えられる。子どものこころを教育的に考えることのできる校長なら、いきなり、「どうしてあんなことを言ったのか」という質問はできなかったのではないか、質問そのものがはじめから重大な問題をはらんでいたとも考えられる。「大嫌いな学校」といったことは、何か理由があるのではないか、自殺への重大なサインではなかったのか?校長も担任もそこに、細心の注意を向けることが求められていたはずだ。テレビでインタビューを受けた子どもたちも、校長は普段の話し方で尋ねていたというが、その内容は、「門出の言葉」は間違っていなくて、この子どもが言い換えたことが間違っているということを前提にしたもので、内容的には詰問になっている。子どもごころには、悪いことをしたと一方的に叱られたと思うのは当然である。私が校長なら、子どもの気持ちになって、その心をときほぐすように、「いじめとか、何かとても悩んでいることがあったんじゃないの?あったら教えて。」「『門出の言葉』があまりいいたくなかったんじゃないの?それだったら誰でも言い換えたくなるかもしれないよね。」というような聞き方をしていたと思う。だいたい、そういうことは、担任によく気を配ってそっときかせるものだろう。私は、教育的というのはそういうことだろうと思う。校長がそのことにまったく気がつかないところに、この学校の悲劇があるのではないだろうか。マスコミでも、この校長の質問のしかたに、まったく注意を向けず、問題を読み取っていないように思われる。この辺に、なぜ自殺を食い止めることができなかったのかという重大なカギが、私は隠されているように思えて残念である。ご訪問有難う御座います。下の2つの教育ブログ・ランキングに参加しています。よろしかったら下のそれぞれのマークをクリックした下さい。ランクの点数が加算されます。人気blogランキングへ
March 27, 2008
コメント(2)
-

学習意欲を本当に引き出す筋道とは?
昨日の夜、さんまの出るテレビ番組で「替え歌大賞」をやっていましたが、それに参加できなかった北島三郎にどうしても弟子入りしたいと思っている大阪の愉快な高校3年生が、特別出演して、卒業式だったが、数学が1科目赤点で卒業延期になったことを替え歌にして歌った。これだけの替え歌が歌える高校生が赤点で卒業できないということは、とても残念で、数学の教え方の方に問題がなかったのだろうかとちょっと疑問に思いました。私は、長年、高校の数学の教師をしていましたが、その授業づくりにおいて大きな力になったのは、小学校の算数や中学校の数学の実践から、たくさんのことを学んだことでした。高校生になると、数学が嫌いという生徒たちも非常に多いわけですが、この生徒たちの学習観や数学観をどのように変えていくのかということは、高校段階の数学の授業にとっては、現在でも非常に重要な課題だと思います。それは、新学期に、数学が好きな人に手をあげてもらっても、手を上げてくれる人は、せいぜい数人しかいないからですね。しかも、好きだという生徒たちも、「計算がすき」だとか「答えがひとつだから好きだ」というものがほとんどだった。しかし、そういうことによっては、数学ぎらいになった生徒たちの学習意欲を喚起することは不可能だと思われます。生徒たちは、何で数学なんかやらなければならないのかと疑問に思っているからです。生徒たちは、公式を覚えて数字をあてはめるのが数学だと考えていたわけだが、それは、ひとことで言えば、操作を覚えるだけの数学ということですね。生徒たちは操作主義の算数や数学にあきあきしているのです。この生徒たちに、あっといわせて、そういうことだったのかといわせることが必要です。そのとき、私が役にたったのが、小中学校の実践から学んだ算数や数学の新しいとらえかただったのですね。例えば、2×3=6という計算を2+2+2=6と答える生徒が少なくない。大学生や大人でも、これ以外の説明が出来る人は案外少ないのではないだろうか?この考え方は、掛け算とは、累加(同じ数を繰り返し加えていくこと)を簡単に表したものということになります。昔、文部省も長い間、こういう教え方を学習指導要領で示してきましたね。しかし、2×3という掛け算は、たんに、同じ数をくりかえして加えるということでは説明できないことが出てきます。例えば、2×0や2×1/2 はどういう足し算としてあらわすことができるか?こうなると、掛け算を足し算とは異なる現実の量の関係を表したものとして、とらえなおすことが必要になります。掛け算は 1当たり量のいくつ分から全体量を求めることととらえると、2×3=6は ハト1匹あたり足が2本で、3匹分では、足は全体で6本 ウォーキング1時間当たり2kmで、3時間分では、歩いた距離は全体で6km同様にして2×0=0は ウォーキング1時間当たり2kmで、0時間分では、歩いた距離は全体で0km2×1/2=1はウォーキング1時間当たり2kmで、1/2時間分(30分)では、歩いた距離は全体で1kmというように、それぞれ具体的な量を用いて楽しく説明することができるのです。今までわかりきっていると思われることがらが、このようにまったく新しい意味があることがわかるとき、生徒たちは、掛け算の新しい世界を発見することになり、掛け算そのものが本当にわかるということと同時に、わかっていると思ってきたことに、思いがけない新しい意味がある、掛け算の楽しい新しい世界を発見することができるのだということを知ることを通して、ものごとを学ぶということの意味がわかるようになるのです。じつは、このことは、教師になった私自身の数学観や学習観を180度変えていく大きな契機になったことでもありました。目からウロコだったのですね。学ぶということは、こういう本質がわかることでなければいけない、学力というものが、こういう本質がわかるという内容をもっているものでなければならないということが、私のその後の授業づくりの方向を決めることになりました。学力低下を叫んでいる人たちには、こういう重要な学びの内実をいうものがまったくわかっていないようにおもわれます。ドリルをいくらいっぱいやっても、いくら競争でけしかけても、こういう本質的な学びには発展しないということがわかっていないのですね。今の日本は、学力を本当につけていく筋道からはずれているとしかいえませんね。私は、小中学校の算数数学の実践から学んだような授業をしたいという思いが強くなり、それが、高校における微分積分の授業づくりに発展していきました。たんに微分積分の公式を覚えて、数字をあてはめて計算ができればいいのではないのです。「小学生でも微分積分ができるようになる」ということを自慢にしている塾もあるらしいけれども、それは、たんに公式を覚えて操作しているにすぎないのであり、本質や意味の分かる学び方をしなければ、本当にわかったとはいえないのではないでしょうか。私は、先輩たちの実践に学びながら、微分法の本質は分析するという方法、つまり、細かく分けていくという方法を使っていることがわかり、積分法の本質は総合するという方法、つまり、いったん細かく分けていったものをもう一度寄せ集めていくという方法を使っていることがわかり、そういうやさしい方法を使って、威力のある微分積分の公式がつくられていくということの面白さがわかる、そういう授業づくりをすすめました。こういう学び方をすれば、生徒たちは、何のために学ぶのかということもだんだんわかっていくのですね。それは、大嫌いだった高校生たちの学習観や数学観をひっくりかえして、いつのまにか数学大好きという生徒たちをつくっていくことにつながっていきました。学習意欲を本当に引き出す筋道は、競争などではないのですね。詳しくは拙著「新・学力への挑戦」をご参照ください。ご訪問有難う御座います。下の2つの教育ブログ・ランキングに参加しています。よろしかったら下のそれぞれのマークをクリックした下さい。ランクの点数が加算されます。人気blogランキングへ
March 24, 2008
コメント(4)
-

若い先生たちの困難と希望 PART5
若い先生たちの困難と希望<PART5>ー雑誌「教育」4月号から学ぶー5.F先生(公立小 男性 1年目)R君(2年)の様子 4月、自己紹介のときは、小さな声でやっと名前を言った内気そうな子だったが、授業中少しずつ立ち歩くようになり、初任研の出張中に学校を抜け出す。その日を堺にして、「むっり!!きょっひ!!」「あっそ、よかったね」「かっこつけ」「こっちみんといて」「こっちばかりこんといて」「くさいねん」と言い、興奮して叫びながら「なんで先生がきめんねん!!」「こんな学校やめたるからな!」「死ね!」と憎々しいまでの表情で暴言を投げつける。授業を始めようとすると運動場にいて、追いかけるとフェンスを乗り越えて外へ!Rに、けられた、たたかれた、死ねって言われた、という子隣のクラスに入り込んで、落書きをしたり、体操袋を窓から落とす。F先生の様子Rは阪神タイガースの大ファン。僕も阪神ファン。Rとつながるには、野球しかないと考えたが、運動場は野球禁止。生徒指導の先生に相談すると、「教材やって考えたらええやん。授業でわかりやすくするためにいろいろ持っていくやろ。野球もそう思ってしたらええやん」と言われてひらめき、新聞紙でバットとボールを二人で作ってグランドへ。野球をしているときのRの表情は、あの挑発的な憎々しいまでの表情が消え、子どもらしい表情に変わり、ニコッとほほえんで「先生!」と言って、新聞ボールを投げ返してきた。「問題児のR君」だけでなく、「かわいらしいR君」に出会うことができたという。昼休みが終わった後、Rが「トイレにきて」と呼びにきたので、行って見ると、そこには流されていない大きなうんこ。F「すごいおおきいりっぱなうんこやなあ」F「これ、Rがしたんか?」R「うん」と少し照れる。F「給食もいっぱい食べるから、うんこもいっぱいなや。流して行こうか」次の日、Rは、また呼びにきたのでついていくと、Rは「先生そこでまっててな」と言い、個室に入っていき、中から「先生!いてる?いてる?」と何度も言う。終わった後、また二人で一緒に大きなうんこを眺めた。次の日、Rは、また、「先生、一緒にトイレに来て!」と呼びにきた。F「なんでいつも先生についてきてって言うの?」R「僕、恐がりやねん」F「Rは恐がりなん?」R「うん」F「そっか、じゃあちゃんとRのうんこがおわるまで、先生待ってるわな」しかし、Rの暴言や挑発的な態度が目に見えて減ってきているわけではない。F先生のうんこの話を聴いてくれた子育て中の先生が、「自分の子どももそういうことがあった。もっと小さいころやけどね。R君は、お母さんとそういうやりとりが、なかったのかもしれないね」と話してくれた。F先生は、その話を聴いてから、Rの起こす事件や、行動への疑問、そして、新しい姿の発見の中で、Rはもしかしたら、ほんとに小さな1つひとつの経験をしてきていないんじゃないだろうかと思うようになり、荒れている姿は2年生だが、それよりもっと幼い子どもだと心がまえて対応していくうちに、Rの「なんで○○やねん!」が、「なんで○○なん?」に変わってきたという。F先生は、Rとの関係もやりとりができるほどによくなってきているが、「先生の言うこと聞いても全然かしこならへんやん」というRのことばをうけとめ。Rの「ほんとうのねがい」にこたえられる教師をめざしているという。・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・PART1~PART5まで、「若い教師たちの困難と希望への筋道」について書いてきましたが、そのひとつひとつの困難の大きさを学ぶと同時に、こども理解の深さは、すばらしいもので、私が改めてふれるまでもなく、ベテランの教師と言われる人たちを超えているのではないかと私は感動しました。そこに、若い教師たちの希望が見えてきます。そして、そういう若い教師たちの困難に耐え、自己変革と教育実践への意欲が、サークルや職場の先輩等とのさまざまな形のつながりやはげましとアドバイスによって生み出されてきていることに注目していきたいと思いました。困難は大きいけれども、現実を人間らしく切り開いていく希望もある!若い先生たちに期待したい!!詳しくは、ぜひ、雑誌「教育」4月号をご参照ください。ご訪問有難う御座います。下の2つの教育ブログ・ランキングに参加しています。よろしかったら下のそれぞれのマークをクリックした下さい。ランクの点数が加算されます。人気blogランキングへ
March 23, 2008
コメント(0)
-

若い教師の困難と希望<PART4>
若い先生たちの困難と希望<PART4>ー雑誌「教育」4月号から学ぶー5.E先生(公立中 男性 ?年目)3年前の生徒たちの様子チャイムが鳴ったら、まず入室指導に悪戦苦闘する。廊下に寝転がってハーフパンツをちらつかせながらダベッている女子をやっと教室に入れる。教室の中では男子がほたえあって暴れている。席に着かせて授業を始めるが、授業が面白くなければ生徒たちは眠ってしまうか、しゃべりはじめて自分たちの世界に入る。そのうちトイレに行きたがる生徒が増え、トイレから帰ってこなくなる。3年前のE先生の様子E先生は、イライラはつのり、笑顔が消え、しゃべり方は講義調になり、「ここがテストに出るんや!聴いとかな知らんで!」と脅す。そして、黒板を何回も消さないといけないほどたくさんの板書を視写させ、教科書を写し、重要箇所に線を引き、訳を書いていく授業をしていた。ある日、板書を終え振り返ると4分の3の生徒が机に突っ伏して眠っていた。E先生の今E先生は、これではいけないと研修会に出かけたり、教育関係の書籍を買ったりしていたが、テレビで田尻悟郎氏の授業に出会い、子どもたちが楽しそうに学んでいる映像を見て、「こんな授業をしたい」と授業改革を取り組み始めた。今、実物として、「My Treasure」を見せながら(show)、そのものについて語る(tell)一人数分の『Show & Tell』 を授業を取り入れてみた。「My family」が「My Treasure」だというトップバッターのN君が次のように締めくくった.This is my mother.She died when I was 12 years old.I was very sad.And ・・・ah,She lives in my heart.That’s all.その時、クラス中からため息がもれ、ある女の子は「涙出るわ」と言い、英語を書くのが苦手な子どもたちも、必死に自分のことばを探して、感想を書いたという。E先生は、心が動く授業は、生徒にも教師にも元気を与えると言う。
March 22, 2008
コメント(0)
-

若い教師の困難と希望<PART3>
若い先生たちの困難と希望<PART3>ー雑誌「教育」4月号から学ぶー4.D先生(公立小 女性 4年目)O君とP君のこと(学年不明) O君は、いつも気に食わない顔をして授業を受けていた。当たり障りない対応をしているとますます悪化し、クラスが崩されていった。D先生は、その子にちゃんと向き合わず逃げていることに気付き、話しかけ、お互い口に出さなければ状況は前進しないことを伝えると、案外すんなりいろいろ話してくれて、彼の不満の原因がわかった。 ところが、最初とてもなついてくれていた、手のかからないと思っていたP君がO君との関係が良好になってきたころ、荒れ始め、「私ね」と平気でくちに出し、噛みつき、手当たり次第に暴れはじめ、とうとう自分を傷つけ始め、「先生なんか大嫌いだ」と言うようになった。D先生は、P君の行動を抑えるのに必死となり、絶望的な気持ちになったが、サークルの仲間に相談、「荒れるS君は何が苦しいのか」と考えられるようになり、Pくんが振り上げた手を握ったとき、振りほどこうとしながらも、離そうとはしないことを通して、「手がかからないからと放っておいた」自分に気がつき、P君の寂しさと本心を感じ取り、手のかからない子に目を向けることの大切さを学んだという。<PART4 に続く>ご訪問有難う御座います。下の2つの教育ブログ・ランキングに参加しています。よろしかったら下のそれぞれのマークをクリックした下さい。ランクの点数が加算されます。人気blogランキングへ
March 20, 2008
コメント(0)
-

若い先生たちの困難と希望<PART2>
若い先生たちの困難と希望<PART2>ー雑誌「教育」4月号から学ぶー3.C先生(公立小 女性)(1)その1(1年目 3年担任) 生徒たち(3年生)の様子 「子どもだもの、これぐらい・・・」と思っているうちに、授業中に勝手なことを言う生徒がふえ、保健室に行く子が続出し、だんだんと統制がきかなくなる。朝7時から夜10時まで学校にいる毎日だった。(2)その2(2年目 2年担任)生徒たちの様子(2年生)の様子 19人のクラス。朝、職員朝会を終えて教室に向かうと、評議員会名と物の倒れる音・・・ドアを開けると、担任の机のものがすべて床に落とされ、壁の掲示物が破られ、もみ合いになっている男の子たちと、逃げ出す準備をしている女の子たち。M君 友達とかかわるのが苦手、自分だけの理屈で友だちに嫌なことを言ったり、いきなりたたいたりするということが日常的にあった。相手が二人いじょうになるとパニックを起こし、教室が滅茶苦茶になることもしばしば。N君 授業中は友だちの発言や教師の話に平気で口をはさみ、ふざけてばかり。とくにU君へのちょっかいが止められない。C先生のとりくみ 5月に1日に「。」3つ(3文)の日記を始める。N君は毎日、「お返事書いた?」と確認しにくる。双子の一人。片方は国立大付属小へ行っており、劣等感と寂しさをもち、乱暴さとなって表れると考える。子どもがよくないことをしたとき、正論で押さえ込んでいたが、それでは子どものこころに届かないと気付き、自分の感情を子どもたちに伝えることにした。 子どもの声に耳を傾ける努力をしたことも、私と子どもの距離を縮めてくれた。●4月から私に打ち解けず、反発することの多かったO君が最後のお別れ会で「お笑い先生も一緒にやろうよ」と台本をかいてくれた。●N君は、イギリスに転校することになったが、終了式後、昇降口で私の足にしがみついて泣き崩れた。<PART3>へ続くご訪問有難う御座います。下の2つの教育ブログ・ランキングに参加しています。よろしかったら下のそれぞれのマークをクリックした下さい。ランクの点数が加算されます。人気blogランキングへ
March 16, 2008
コメント(0)
-

若い教師の直面している困難と希望への道筋
若い先生たちの困難と希望への道筋<PART1>雑誌「教育」4月号は、若い先生がたが、今の教室で、子どもたちのどういう現実と向かい合っているのか、そして、困難とどのように格闘し、希望を見出そうとしているのかという報告を特集している。以下のメモは、学校現場で今何が起きているのかということをリアルに理解していくために、若い先生方の報告を自分なりにまとめたものです。詳しくは、「教育」4月号をご覧ください。わたしの感想を一言でいうと、想像以上に困難な事態が教育現場では進行しているということであり、若い教師たちのかかえているこういう現実を、先輩教師・親や地域、教育行政関係者等は、本当に理解し、様々な支援を考えていかなければならないのではないかということです。この報告をした先生がたは、そういう点で、先輩教師とともに若い先生方が集まり話し合い、学びあうネットワークをもっているということが、それぞれの困難を乗り越えていく原動力になっているのではないかと感じられます。1.A先生(公立小1年目 5年担任、男性)の報告からL君の様子 最初の頃はよく発言する活発な子だなと思っていたが、自分勝手な行動や教師に対する暴言が始まる。わがままな行動を注意されると反発。「お前なんか教師やめちまえ」「お前が担任やってるからつまんねーんだよなぁ」と言う。授業中は図書館から持ってきた本を読み、社会の地域探検で外に出たときには他の子を鉛筆で刺す。友達には命令したい放題。A先生の転機 「減点法から加点法」「良いところを見つけよう」と思えた時、子どもたちのがんばりに目がいくようになり、3学期にはクラスが落ち着きをとりもどす。2.B先生(公立小1年目 2年担任 女性)の報告から M君の様子 その1 求職の最中に、おぼんごとひっくりかえす。掃除の時間には机を倒し、お道具箱をひっくり返す。窓に走っていき、「飛び降りてやる!!」と言う。友達とトラブルになると物(鍵盤ハーモニカ)を投げる。B先生の対応 子どもたちの声をちっとも聴いていない自分に気がつく。とにかく聴こうと努めた。M君の様子 その2 2年後、5年になったB君の担任に。1学期には鎌倉遠足で石をいろいろなところに投げ始め、「どうしたの?」ときくとうずくまって固まる。また、いきなり鉛筆を折ったり、夏の林間学校では2時間も固まったまま動かなかった。 そのたびに、場所を変え、気持ちが整理できるまで待つ。それから、何が嫌だったのか話を聴き、答えられない場合は選択肢をあげて一緒に考えていくようにした。問いかけに頷いたり、首を振ったりするようになり、固まってしまうことも少なくなってきた。<PART2 へ続く>ご訪問有難う御座います。下の2つの教育ブログ・ランキングに参加しています。よろしかったら下のそれぞれのマークをクリックした下さい。ランクの点数が加算されます。人気blogランキングへ
March 15, 2008
コメント(0)
-

今夜の学力問題をめぐるNHKの長時間番組
今夜、3時間の長時間テレビ番組があります。NHKの「日本のこれから 『大丈夫ですか?日本人の学力』 技術立国の危機?市民40人大激論」です。こういうタイトルで、学力問題をとりあげるのですが、その内容は、次のような形であらかじめレールが敷かれています。▽ 携帯にはまる子供・分数のできない大学生・マニュアル頼りの社員VS大人の学力こそ問題▽ 落ちこぼれ救済か?エリート養成?揺れる学校現場▽ 勉強なんて意味ない?格差社会で自暴自棄に▽ インド・中国の足音が・・・日本沈没?学力復活の鍵はタイトルそのものが、はじめから「技術立国の危機」と学力問題に大きな枠をはめるとともに具体的テーマも上のように設定されていますから、「大激論」の大きな方向は、決められていて、司会はそれにそったすすめ方をするだろうなあと感じるのですが、重要なことは、これによって、人間丸ごとの発達の危機という問題が番組から欠落してしまうことです。このような一面的・皮相的な「危機」のとらえ方から出発する学力問題に関する番組づくりは、そもそも誰にとっての番組づくりなのかという疑問が生まれるものであり、小中高校生たちの人間発達の深刻な危機から目をそらす役割を果たすものになるのではないでしょうか。私がこのようなことを言うのは、私自身の苦い体験にもとづくものです。私は、中3の1学期に会津から東京の○○中に転校して、昭和30年に、新設5年目の都立M高校に入りました。進学実績をあげて学校のランクをあげようとしていたこの新設高校は、ひそかに成績のよさそうな生徒たちを集めた1クラスをつくりましたが、私もそこに入っておりました。高校生の私は、そのことに違和感はもちませんでした。ただ、1年から2年に進級するときに、中学から一緒だった友人が成期がおもわしくなくて、別のクラスに落とされたことが、心に傷としてのこりました。そのクラス担任が数学の教師で、機会があると剣聖宮本武蔵の修行を説き、競争に勝つ心得を諭しました。その中心は、周りの人たちを「雑魚」(ざこ)とみなし、「雑魚に目をくれるな!わが道を行け」というものでした。この教えを素直に受け入れた純真な?私は、わき目もふらず、クラスの係りも逃げ回り、遠足もくだらないと参加せず、高校時代に一人の友人もつくらず、剣聖のような孤高?の―孤独の―高校時代を過ごしました。そのあげくに、大学受験に3回も失敗し、家庭の事情もあって、私立大学は受けることなど考えられず、さらに3年もの孤高?の修行時代、浪人時代をおくりました。そんなわけで、私は、授業そのものがわからないという問題と同時に、人間や人間関係そのものを否定する考え方をもつようになり、その結果、大変刹那的な考え方をするようになり、そういう刹那的な考え方から出発した生き方を模索する危険な状態になっていきました。競争の教育のもたらすそういう人間をゆがめてしまう側面をくぐってきた私としては、その時代とはくらべものにならない競争の激化、競争の低年齢化のもとで、現在の教育のありように深い危惧をもっているのです。NHKが公共放送として学力問題をとりあげるならば、人間発達の危機としての視点は討論テーマからもはずすべきではないでしょう。また、学力の内容とともに、それにかかわる競争の教育そのものを正面から問う討論も不可欠です。今夜の長時間番組が、 競争の教育を排して技術立国を果たしているフィンランドの教育を,NHKが討論の素材としてどのように取り上げていくのかも見ものです。NHKが本当の「学力復活の鍵は?」を、提起する番組となることを祈るばかりです。ご訪問有難う御座います。下の2つの教育ブログ・ランキングに参加しています。よろしかったら下のそれぞれのマークをクリックした下さい。ランクの点数が加算されます。人気blogランキングへ
March 8, 2008
コメント(1)
-

リンの写真館 その3
リンの写真館 その3今から11年ほど前の幼い頃の写真です。拾われてきて2ヶ月ほどたった頃の写真です。命の鼓動が聞こえます。青い毛布の上で身構えるリンコタツでウトウトしているリン青い毛布にくるまれたリンリンの写真館 その1リンの写真館 その2ご訪問有難う御座います。下の2つの教育ブログ・ランキングに参加しています。よろしかったら下のそれぞれのマークをクリックした下さい。ランクの点数が加算されます。人気blogランキングへ
February 16, 2008
コメント(3)
-

なぜ、T君は答案に答えだけしか書かなかったのか?
Katakuriさんとkatakuri mama さんからのすばらしいコメント昨日,私が出した<問題>に対して、Katakuriさんとkatakuri mama さんのお二人から、すばらしいコメントが寄せられました。お礼を申し上げて、ここで改めて紹介させていただきます。Katakuriさんは、現在15歳です。くわしくは ホームスクール リベラ実践記 へどうぞ。Katakuriさんのコメントa/x+b/y=(ax+by)/xyと計算したのだと思います。正解した問題は分子が等しいので上の式のように計算しても正しい答えが出ます。結局通分の意味がわからず計算方法を間違えて覚えていたのだと思います。Katakuri katakuri mama さんからのコメント分数の意味が、イメージとしてわかっていないんでしょうね。分数・通分も水道方式の図で表すやり方はとてもわかり易いのだけれど実際のイメージが伴わず数字の操作だけしてしまうと、こういう珍答が後を絶たないのでしょうね。プロセスがだいじなのですが、このケースではそれ以前の分数そのものの理解に問題がある気がしますがkatakuri mama私の出した問題は次のようなものでした。<中学1年生の答案>1. 1/2+1/3 =5/6 2. 2/3+1/5=11/153. 2/5+2/7=24/354. 3/7+2/5=31/35<問題>まず上の4題を解いてみて答えあわせをしてください。そして、この中学1年生は、なぜ、途中の式を書かなかったのか考えて、あなたの考えをのべてください。さて、この<問題>に対する答えですが、私がこのときどうしたのかということをお話して、答えにしたいと思います。この中学1年生をT君という仮名でお話します。 じつは、T君に出会ったのは、以前、私の住んでいた地域で、知り合いのお母さん方から、算数や数学ができなくて困っているのでみてほしいと言われて、気軽に引き受けてしまったのですが、日曜日に会場に行ってみたら、小学生など20人近くが集まっていたのです。その中にT君もいました。私は、何気なくT君の答案に○×をつけていて、とても答えだけの答案に何か変だということを感じました。そこで、T君に、「途中の式を書いてみて」といいました。T君は、しばらく書こうとしませんでしたが、ようやく最初の問題の計算式を書いてくれました。その式を見たとき、私は、信じられませんでした。1/2+1/3=2/6+3/6=5/6と書いたのです。「えっ!どうして 1/2が2/6になるの?」と聞くと、T君は、鉛筆で数字を指しながら、ぼそぼそと両方の分母をかけて新しい分母をつくること、そして、分子は、自分の分母の2と分子の1をかけて2にすると言いました。そこで、1/2は2/6 と直したのです。そうすると、1/3は3/6 に直して、1/2+1/3=2/6+3/6=5/6となり、5/6という正しい答えにたどりついていたわけです。「なるほど~!」私はびっくりしてしまいました。それでやっても、確かに正解になるからです。そういう解き方もあったんだあ!すご~い!答えだけ書くなら、T君方式だっていいではないか??でも、この解き方は、両方の分子が同じ時にしか正解にならないのです。1/2+2/3 などとなると間違った答えになるのです。このいきさつを、katakuri さんは、じつに簡潔に説明してくれたわけです。ところで、私の出した<問題>の後半には、さらに、「T君は、なぜ途中の式を書かなかったのかを考えて、あなたの考えをのべてください」とあります。そこで、これまで解明してきたことをもとに、T君が途中の式を書かなかった理由を考えてみたいと思います。 私の想像では、中学1年生になるまで、T君は、分数が魔物のように見えたのではないかと思うのです。 なぜなら、同じやり方をしているのに、あるときは○になり、あるときは×になるからです。でも自分の覚えた計算方法は、これしかないのですから、分数の加減ということになりますと、この方式で解くしかなかったのです。しかも、悲劇は、○をもらったところこそがじつは間違っていたということです。 これでは、どんなにどっさり宿題を出してもらっても、T君にとっては何の役にもたっていなかったことは言うまでもありません。 T君は、小学校時代、ず~っとわけのわからない○と×をもらい続けてきたわけですから、自分の考えを式という形で表現する自信を完全に失っていたのではないかと思うのです。 途中の計算式のない答えだけの答案は、こうして生まれたのです。やはり深いわけがあったのです。 それは、T君の問題というよりも、現在の教育のもっている深刻な問題がこういう形で現れてきているというように見た方がいいのではないかと思われます。 Katakuri mama さんが指摘されたように、分数そのものから、わかるように教えることを大切にする学校や先生だったら、あるいは倍分ということをしっかり折り紙などで教えてくれる学校や先生だったら、T君の間違い方に法則性があるということに気がつき、もっと早く気がついて直してあげることができたかもしれませんね。 私は、このような教育の中で、かえって子どもたちの自信を失わせていくことがあるという事実を知っていただきたいなあと思います。 いろいろな国際比較で、日本人には自信が足りないという結果がでてくる背景には、自信を失わせる教育が広がっており、それが、教育内容の質とかかわっているのではないかという疑問をもつことが大切ではないでしょうか。 今、学力問題ということで、算数ではドリルをどっさり宿題にだすなどということが、何か一生懸命やっている学校や先生みたいに見られる風潮さえある中で、改めて、何をどのように教えるのかという原点から、教える内容、質を問い直さなければならないと思うのです。 今日、文部科学省は、新学習指導要領を発表し、担当大臣の記者会見もありましたが、ゆとり教育は間違いで、小学校でも算数の教える内容や時間をふやすというようなことが報道されていますが、一番大事な教育の質の問題は検討されず、なおざりにされたままでしたね。 余談になりますが、T君の間違いは、授業の中に発見できれば、みんなで考えて、分数計算を深く理解する非常に面白い問題になると思うのです。 50歳を超えたスタンダールというフランスの小説家は、マイナス×マイナスがプラスになることを、「借金×借金=財産 になるということは、どうしても理解できない。10万円の借金と5万円の借金をかけると、なぜ50万円の財産になるのか」と頭を悩ませたといいます。(遠山啓著『数学入門』上 66ページ 岩波新書) 考えてみると、T君の悩みは、このスタンダールの悩みに匹敵するほど大きなものだったのではないでしょうか。 Katakuri mama さんから追加のコメントを頂いておりました。私の言いたいことをもっともっとよく整理していただいておりますので、ちょっとずるいのですが、紹介してまとめにしたいと思います。私の答え 付録版!! シューレ・リベラさん もう一つ、このケースで気になったことがあったので追伸です。 こういうケースで困るのは、まぐれでこのように当たってしまうので、本人も親もあるいは教師も、この子は50%は出来るんだと思ってしまうことなのです。 実は、彼(彼女かな)はそもそも分数についても、通分の意味もほとんどわかっていない・・その意味では零点なのだけれど、何となくみんながその点を見過ごしてしまい、わからない事がどんどん積み上がって、基本のぐらぐらな、とても脆弱な「数学」という建物ができあがってしまうことだと思うのですが。 しかも困るのは、遠山先生も指摘しておられたように、わからないのに出来てしまう子どもが、年と共に増加している点です。 「○○式」に代表されるような、わかってないのに、数の操作だけ覚え込ませるトレーニングの増加もそんな現象に拍車をかけているのだとおもうのですが・・。ご訪問有難う御座います。下の2つの教育ブログ・ランキングに参加しています。よろしかったら下のそれぞれのマークをクリックした下さい。ランクの点数が加算されます。人気blogランキングへ
February 15, 2008
コメント(2)
-

途中の式がまったくない分数計算の答案
ある中学1年生に簡単な分数計算の問題を10題ほど出したことがあります。そしたら、答案用紙には途中の式が書いてなくて、答えだけを書いていました。普通なら通分して計算する過程を書きますよね。私は、きっと、余白に計算して、それを消してしまったのだろうと思いました。そういう生徒が結構いるのですね。私は、高校1年生で、定期テストのときに、=がまったくない答案をみたこともあります。この生徒には、=をつける意味を1年間指導して直したことがあります。私は、途中の式が大事なのになんで消してしまうのだろう、見直すときだって必要なのにと思いながら、採点をしてみました。そしたら、多分、3~4割ほどできていました。その問題と答案はこんな具合でした。<中学1年生の答案>1. 1/2+1/3 =5/62. 2/3+1/5=11/153. 2/5+2/7=24/354. 3/7+2/5=31/35 ・・・・・・・・以下略さて、問題です。<問題>まず上の4題を解いてみて答えあわせをしてください。そして、この中学1年生は、なぜ、途中の式を書かなかったのか考えて、あなたの考えをのべてください。解答はコメント欄にお願いいたします。正解は次回予定です・・・ご訪問有難う御座います。下の2つの教育ブログ・ランキングに参加しています。よろしかったら下のそれぞれのマークをクリックした下さい。ランクの点数が加算されます。人気blogランキングへ
February 14, 2008
コメント(4)
-

『母べえ』と2つの限りなく美しい“窯変”
昨日、dreem21どんさんから『母べえ』を「本屋で立ち読みでもしたら」とアドバイスいただいたので、早速今日は、午前中、本屋にちょっと立ち寄ってきた。 じつに明るい愛らしい装丁の野上照代原作の『母べえ』。 その前書きに、山田洋次監督の映画「『母べえ』の製作にまつわる話がのっていた。 そこにさっと目を通すと、最後の方で私は、ひとつのことばに釘付けになった。 それは“窯変”ということばであった。それは、私が昨日書いた日記ともかかわるこの映画を読み解く大切なキーワードだと思った。 試写室で山田洋次監督が作品を観たとき、自分がひたむきに描いてきた家族というものの向こうに、思いがけず戦争に突入していく時代というものがくっきりと描きだされてきていたということに驚き、そのことを、“窯変していた”といったのである。 山田監督は、黒澤明監督が「映画は窯変することがある」ということばをよく使っていたことを紹介しつつ、『母べえ』という作品が、その“窯変”をしていたと試写の感想で書いているのである。 私は、ここに山田監督の真骨頂を見た思いがする。 つまり、“窯変”としてその時代をも描き、まさに渾然一体の作品に仕上げていたのである。 “窯変”とはインターネットで調べると、焼き物をしたときに現れる陶芸家も予期・予測しきれないような、窯から出してみないとわからないような思わぬ絶妙の焼き上がりとでもいうことができるだろうか。 さて、この原作者の野上照代さんは、1951年以降の黒澤明監督の全作品に参加された方だという。84年、自伝的少女時代の家族を描いた「父へのレクイエム」が07年12月『母べえ』として出版(中央公論新社)され、また、今回の映画『母べえ』となったものだが、野上さんは、この映画の公式サイトで、自分の『原作』から映画『母べえ』が生まれたことを、山田監督と同じく、黒澤明監督の同じことばを引用して、“窯変”していると評していることにびっくりした。■原作者(注 野上照代さん)の言葉「映画は窯変することがある」と黒澤さんは言う。陶磁器を窯の火焔からとり出す時、予期しなかった美しい色に変色していることだ。私の粗末な素材は、窯変して「母べえ」となった。山田洋次監督のプロの腕によるものである。 私は、dreem21どんさんのアドバイスを受けて、本屋さんで立ち読みしたことがきっかけで思いがけず、2つの限りなく美しい“窯変”に出会うことができた。 いいことばだ。少しむずかしいけれども、“窯変”という漢字を書く練習をして、美しく書けるようになっておこう。 立ち止まって考えてみると、学校や教室というところは、本来、教師が考えている以上に子どもたちの目を見張る変化、“窯変”を生み出す場でなければならないのではないだろうか。 そういうところから胸を痛める現実をみるとき、今日もひたむきに子どもたちのために悪戦苦闘している教師たちに、そして、健気に生きている子どもたちに希望をたくしながら、今、自分でやれることを少しずつとりくんでいきたいと思う今日の日である。ご訪問有難う御座います。下の2つの教育ブログ・ランキングに参加しています。よろしかったら下のそれぞれのマークをクリックした下さい。ランクの点数が加算されます。人気blogランキングへ
February 13, 2008
コメント(2)
-

『母べえ』は「家庭」を通して時代を描ききれているか
今日、近くの映画館で10時45分から「母べえ」を観てきた。山田監督が挑んだこの作品に深い感銘を受けた。テレビでは、山田監督が、吉永さゆりに長い手紙を書き、母べえ役をたのんだとき、「やらせていただきます」との電話が来たとき、この映画が半分成功したようなものだと語っていたが、たしかに吉永さゆりの演技は、みごたえがあった。同時に、その他の配役の演技も見事だった。『母べえ』公式サイトはここをクリックしかし、すばらしい作品だからこそ、思い返してみると、戦前というわれわれが現在を考える原点にすべき時代をどれだけリアリティをもって描くかという点で、2つばかり気になる点があった。1つ目は、隣組などが組織された小さく閉じられた社会の中で、夫が特高によって逮捕された母べえの家に通う夫の教え子の徴兵検査をまぬがれていた青年山崎の姿の描き方である。山崎が母べえの家に通う情景には、近所の小うるさい好奇の目というものがまったく描かれていないことである。2つ目は、治安維持法下、教育勅語のもとに行なわれた皇国民の練成という教育の情景やその矛盾が、代用教員として小学校の教壇にたつことになった母べえを通してや、その学校で学ぶ二人の子どもを通しても、まったく描かれていない、捨象されていることである。この問題は、母べえが特高によって思想犯として逮捕された夫を深く理解する重要な契機になりうるはずなのに、まことにおしいことだと思った。私のブログでは、2006年6月24日の『純情きらり』―笛子の最後の授業ーとしてとりあげたような教育の緊迫した矛盾というものが、良識をもつ人々すべてに容赦なくあらわれていたはずだからである。 『純情きらり』―笛子の最後の授業ーはここをクリック山田監督は家庭を通して、時代というものを語りたかったのだと思うけれども、まさにその家庭の上に避けがたくおそいかかってきていた教育勅語が支配する教育の矛盾というものを通して、時代を語るということをしなかったのはなぜか、避けたのか、作品として捨象しうるものであったのか、原作の限界だったのか、時間の制約だったのか…ということが、私の中には大きな問いとして残った。どなたかご意見をお聞かせください。ご訪問有難う御座います。下の2つの教育ブログ・ランキングに参加しています。よろしかったら下のそれぞれのマークをクリックした下さい。ランクの点数が加算されます。人気blogランキングへ
February 11, 2008
コメント(6)
-

私がこの家にくらしはじめたワケ
私が小さかった頃 リン今から11年ほど前の秋ごろ、私は、保育園の隣の取り入れの終わった田んぼのあぜ道から、小さなカゴに入れられてこの家にやってきました。1996年10月のことです。名前をリンとつけられました。そう、私は女の子です。名前をつけたのは、私をひろってきた奥様です。ご主人様は生き物を飼うのはいやだといいました。そこで奥様はほんの2、3日だけちょっとおかせてと言いました。2、3日が1週間になり、1週間が1ヶ月になり、1ヶ月が1年になり、そして、とうとう1年が11年になってしまいました。11年前の私は、こんなに幼かったのですよ。ご主人さまと奥様では、私に対する態度が少し違います。ご主人さまもはじめはいやだと言っていましたが、根はやさしい方のようで、私の良き遊び相手になってくれますし、私の気持ちをとてもよく理解してくれるところがあります。そういうわけで、私の心から少しずつ恐怖感というものがなくなって、この家で暮らしてもいいかなあという気持ちが芽生えてきました。ご主人さまは長らく高等学校というところの先生というものをされていたようですが、ことばも話せない私の気持ちを理解するのと同じように、生徒さんの気持ちというものも理解しなければならないのだとおっしゃいます。それが、学校というところの原点だというのですが、ネコの私にはむずかしくてわかりません。ご訪問有難う御座います。下の2つの教育ブログ・ランキングに参加しています。よろしかったら下のそれぞれのマークをクリックした下さい。ランクの点数が加算されます。人気blogランキングへ
February 10, 2008
コメント(2)
-

わが家のネコ リン
はじめまして わが家のネコです。名前はリンです。たんぼのあぜ道でひろったネコです。人見知りするネコです。なきかたを親から習わなかったのかもしれません。ようやく、静かに可愛い声で鳴くことを覚えました。お客さんがくると隠れてしまいます。何年たっても30秒も抱かれていません。毎日、家中を探検し、新しい昼寝の場所を探します。ブログにさっそうとデビューです。よろしくおねがいします。ご訪問有難う御座います。下の2つの教育ブログ・ランキングに参加しています。よろしかったら下のそれぞれのマークをクリックした下さい。ランクの点数が加算されます。人気blogランキングへ
February 9, 2008
コメント(2)
-

40年前の卒業生からの手作り味噌の贈り物
今から40年もまえの1960年代末に卒業したTさんから、手作りの味噌と知人からとりよせたという自慢の卵がどっさり届いた。味噌は麹の多めのものと普通のものが同じ容器の中に半分ずつつめられていた。卵の消費期限は1ヶ月、黄身は色鮮やかでぷっくりとふくらんで存在感を示していた。 今、我が家の食卓には、毎日、大根の味噌汁と卵料理が並び、安心安全の豊かな食事が続いている。日本中が餃子問題で食生活が脅かされている中で。 私が女子高の教師になって2年目、Tさんは高校3年。私は、担任でもなく、数学を教えたわけでもない。私が生徒会顧問だったことから、多分、演劇部の部長をしていたTさんを学園祭の準備などを通して知るようになったのではないだろうか。この部長さんは、どうも裏方が好きだったようだ。Tさんが仕切った送別会のピーターパンの出し物は、抱腹絶倒で大成功を収めたことが思い出される。 このTさんの親友に生徒会の会長だったHさんがいる。Hさんは、歯切れよくじつにズバズバものを言う人物だった。ある時、Hさんは学校側と鋭く衝突して腹を立て、生徒会長のバッジを私につき返しにきたこともあった。ただ、そのあとどうなったのかはもう今は覚えていない。 二人は今も大親友で、Tさんのもう一人の愉快な演劇部の親友Kさんの3人は、2000年春、私と妻を招いて、定年退職のお祝いをしてくれた。 私がつくづく感じることは、学校というところは、直接担任をしたり、授業を教えたりしない場合でも、こういう人間関係をつくることができるということだ。とくに高校時代にできた友人たちと生涯助け合いながら生きていく姿をみていると、受験にとらわれて、高校時代、一人の友人をつくれなかった自分にとっては、うらやましい限りである。こういう人間関係がつくれたのは、現在とはちがって、当時はまだ、学校が人間的な本来の学校らしさをもっていたからなのかもしれない。 さて、私がうれしいと思うことは、こういう卒業生たちが、それぞれ社会に出て、一人の市民として生きながら、さまざまな人間関係をむすびながら様々な情報を手に入れ、社会の中で市民としての教養を身につけ見事に成長していっているということを感じることができるからである。 国会で、総理が安全・安心を百万遍唱えても、誰もあてにしない時代、市民が自らの目と頭を働かせて取捨選択して生きていく知恵を身につけなければならない時代になった。 そんなときTさんから昨日届いた1通のケイタイメールは、国民をどん底に突き落とす冷たい政治の元で、じつは皮肉にも、その政治そのものが、一人ひとりのいままでの教養のあり方を問い直させ、新しい市民としての教養を身につけさせる先生の役割を果たす結果になっていることを教えてくれる。 進学実績に目を奪われ、競争に駆り立てられている親や学校は、こういう時代に子どもたちにいったい何を教えるべきなのかを改めて深く考えさせられるメールである。新しい学習指導要領の発表も真近のようであるが、一片の期待ももてないのも不思議ではない。 Tさんからの愉快な一通のケイタイメールお寒うございます。メールありがとうございました。先日のメールも、あぁ、そうそう…、生みたての卵は、たしかに温かく、殻で、判断して、貝の殻を砕いて餌に混ぜていたっけ。卵は、ちゃんと卵の味がしていましたね。派手ではないけれど、地に足がしっかりついていた、心豊かな贅沢な食生活を当たり前に思っていました。 いつの頃からでしょうか、食物の表示の中に必ずといっていいほど保存料や、香料、着色料、はては、素材に、ビタミンナニガシを添加…大きなお世話です。 実家に帰ると、農道沿いのあちこちに休耕田があり、あれだけ雑草を蔓延らせては水田に戻すのは、さぞ時間がかかる事だろうと、じいちゃん、ばぁちゃん達が大事に、大切にしていた田畑というのを知っているだけに心が痛みます。 日本は、みずほの国と言われていたのに、自給率が30数%というのはなぜ?こんなことになってしまったのでしょう?食の安全という基本的な事がぐらついていて、これからの子供達にバトンタッチ出来る事がどれほどあるのでしょうか?いや、いや、なんて偉そうに一席ぶってしまいましたぁ~汗、汗、汗。お酒の友を伝授いただいたので、ちょっと、ほろ酔い…。 さて、喜んで下さい。畑は調達致しました。春になったら、蒔物が出来ます。先生にも、少しばかり「食の安全」いえ「安全な食べ物」をお送り出来そうで私もうれしいです。自然相手の事ゆえ、早用はききませんが、お待ち下さいませ。メールありがとうございました。ご訪問有難う御座います。下の2つの教育ブログ・ランキングに参加しています。よろしかったら下のそれぞれのマークをクリックした下さい。ランクの点数が加算されます。人気blogランキングへ
February 8, 2008
コメント(2)
-

子どもたちに 本当の贈り物を
ご訪問有難う御座います。下の2つの教育ブログ・ランキングに参加しています。よろしかったら下のそれぞれのマークをクリックした下さい。ランクの点数が加算されます。人気blogランキングへ
January 1, 2008
コメント(4)
-

『恋空」に共感する女子高校生
「共感できる」と女子高校生たちがいう。進学実績をあげるための「学力向上」の一環として推奨されている朝の読書。テレビは、品川のある女子高校の朝の読書風景を紹介する。女子高校生たちは驚くほど静かに本を読んでいる。「自分の好きな本を持ってきて読んでください」というときの学校の期待。しかし、その期待は意外な方向に展開していることを思い知らされる。テレビのシーンは、その読んでいる本の紹介に。「恋空」読んでいる本はケイタイ小説らしい。「恋空」を手にした高校生は、笑顔ではじめに紹介した言葉を口にする。「共感できる」と。たしかに大人が期待するような静かな読書の時間が流れていくが、それは子どもたちから思いがけない辛らつな復讐にあっているようでさえある。朝の読書の時間がケイタイ小説によって席巻されているからだ。何か似たようなことがあるなあと思ったら、日本の食糧自給率のような問題だなあと感じる。そういうわけで、遅ればせながら、私も「恋空」を検索して10ページほど読んでみた。なるほど、ケイタイ小説というものはこういうつくりになっているのかということを知った。美嘉がヒロキと付き合うことになるまでの4月から9月ごろまでのいきさつが、じつに読みやすく書かれている。私は、中学・高校時代という青春期の共感というものが、本当にこういうレベルのものでいいのかどうかということを考えてしまった。活字離れをなんとかしたい、国語の学力をつけたいということで、推奨されてきた朝の読書時間ではあるが、かえってそのことが、文学における共感ということを知らない若者を育てるためにも、役立ちはじめているように感じられる。むしろ、こんな小説くだらないと共感しない中学生・高校生になってほしいなあと思う。昨夜、戸坂潤の「科学方法論」を少し読んで見て、あまりにも難解で歯がたたなかったことを思い出した。「恋空」を読んで見て、改めて、読みやすければいいというものでもないなと思った。そして、大学受験で浪人していた時代、阿部次郎の「三太郎の日記」を読んだときに覚えた共感の感情を思い出した。ご訪問有難う御座います。下の2つの教育ブログ・ランキングに参加しています。よろしかったら下のそれぞれのマークをクリックした下さい。ランクの点数が加算されます。人気blogランキングへ
October 22, 2007
コメント(0)
-

たとえ醜くても真実を知りたい、学びたい、そして伝えたい!沖縄の高校生の胸に迫る訴え
沖縄で11万人を超える人々が集まった。「歴史をゆがめる教科書検定意見を撤回を求める沖縄県民大会」が宜野湾市で開かれたのだ。参加者数は県民10人に1人の割合に。同じ割合で東京が集会を開いたとすると100万人を超える規模の集会になる。沖縄の人たちの怒りが伝わってくる。「琉球新報」を検索すると、動画をつけて集会を詳細に報道している。http://ryukyushimpo.jp/video/index_20.php二人の高校生の訴えは、胸にひびくものであった。「私たちのおじぃおばぁたちが、うそをついているといいたいのでしょうか」「私たちの住んでいる読谷村には集団自決が起こった『チビチリガマ』があります」「手りゅう弾を配った日本軍は明らかに『自決』を強要している」「教科書から軍の関与を消さないでください。あの醜い戦争を美化しないでください。たとえ醜くても真実を知りたい、学びたい、そして伝えたい」数学で本質を学ぶということと、歴史で事実を事実として学ぶということ、真実を学ぶということは、つながっているなあと思う。高校生の訴えには、高校生が何を学びたいと考えているのかということを、われわれに教えてくれるものとなっている。それは、いい大学に入りたいなどというものではない。「たとえ醜くても真実を知りたい、学びたい、そして伝えたい」というこの要求にこたえることこそ、学力問題を本当に解決していく筋道なのではないだろうか。学力低下を嘆き、学力低下を憂いている人たちには、このもっとも肝心なことがわかっていない。久しぶりに、今日は、教育関係のブログの上位からパラパラと拝見してみたが、案外この問題にはふれていないみたいなので、久しぶりにブログを書いてみようという気になったのだが、みなさんは、沖縄のこの集会をどんな風に思っているのかなあ。ご訪問有難う御座います。下の2つの教育ブログ・ランキングに参加しています。よろしかったら下のそれぞれのマークをクリックした下さい。ランクの点数が加算されます。人気blogランキングへ
October 1, 2007
コメント(3)
-

ガソリンの値上げのニュースで、1当たり量を使っていましたね
今日は、テレビで、ガソリンがさらに値上げになるというニュース。1リットル当たり4円も値上げされるらしい。これからいよいよ帰省や旅行に出かけるシーズンなのに、これは弱った。「満タンにするのがためらわれる」というドライバーの声も紹介されたが、まったく同感。1リットル当たり4円値上げされて147円とかになると60リットル入れると、合計は、147円/リットル×60リットル分=8820円1万円札が吹き飛ぶ!ところで、このニュース、値上げ幅が1リットル当たり 4円とか値上げされて1リットル当たり 147円とか言っていましたが、これが、一昨日とりあげたマイナス×マイナスの中で、掛け算を説明するために取り上げた。1当たり量を使っているということにお気づきになられましたか?とにかく、町中のGSを見てまわって、1当たり量で比較して、ガソリンの安い店を探すしかありませんね。でも、品質には注意して。ご訪問有難う御座います。下の2つの教育ブログ・ランキングに参加しています。よろしかったら下のそれぞれのマークをクリックした下さい。ランクの点数が加算されます。人気blogランキングへ
August 1, 2007
コメント(0)
-

本質がわかる授業とは?(3) 大学生の感想
シリーズ 本質が分かる授業とは?(3) マイナス×マイナスはなぜプラスになるのか等・・・大学生の感想から<正負の掛け算・・・計算のやり方だけを暗記していた> マイナスの数の掛け算を習った時、ただ、自動的に同じ符号どうしならプラスになるというふうに暗記させられただけだったので、今日の先生の説明を聞いて、こういうふうにきちんとわかりやすく教えてほしかったなあと思った。 因数分解の説明も図形を使ったものは見たことがなかったので驚いたし、わかりやすいと思った。 私は数学がとても苦手だったので、なぜそういう風になるのか考えず、計算のやり方だけを暗記していたが、それがかえって数学をわかりにくくしていたのかなあと思った。(Kさん)<先生の授業の核心は、物事の本質をどう読み解くかということを一貫してやっている> 今日の授業は、今までの授業内容と一風変わったものでした。 今までは、総体的な子どもを取り巻く教育関係の内容が多かったですが、今回は、実際の授業において、どのように子どもたちに学びというものを教えるかということでした。 考え方、教え方が今まで私が聞いたり考えたりしたことがないものでとても斬新で、目新しいもので、新鮮なおどろきがありました。 このように初めはそのことのみに目がいっていたのですが、ここで、ひとつの考えが心に浮かびました。 それは、今までの授業も今回のものも、先生は物事の本質をどう読み解くか、どういう実際の事象を考えればよいのかということを一貫してやっているだけで、授業の核心は変わっていないということです。(Lさん)ご訪問有難う御座います。下の2つの教育ブログ・ランキングに参加しています。よろしかったら下のそれぞれのマークをクリックした下さい。ランクの点数が加算されます。人気blogランキングへ
July 31, 2007
コメント(0)
-

マイナス×マイナスはなぜプラスになるの?大特集!
シリーズ「本質がわかる授業とは?(3)」の大学生の感想紹介では、マイナス×マイナスの授業についてもでてきますので、今日は、「マイナス×マイナスはなぜプラスになるのか」ということを改めて取り上げてみたいと思います。大人の皆さんは、この質問に答えられますか。マイナス×マイナスは、なぜプラスになるか? マイナス×マイナスがなぜプラスになるのかは、次の3つの段階をふめば誰でも簡単にわかります。第1段階は、掛け算とは何か、第2段階は、正負とは何か、第3段階 正負の規則はどのようにしてうまれるのか です。第1段階 掛け算とは、3つの量の関係です掛け算とは、次のような 3つの量 の関係を表しています。 1当たり量 の いくつ分 から 全体量 を求めること 例1 6×3=18 はどういうことを表しているのでしょうか? 1当たり量が6のものをまず探しましょう。 アリ1匹あたり足6本とかカブトムシ1匹当たり足6本だとか、バレーボール1チーム当たり選手6人だとか、いろいろなことが思いつくといいですね。 (トンボもセミも昆虫ですから、足はみんな6本ついていますね・どれを使ってもいいのです) こういう表し方をしたものが1当たり量です。時速や秒速なども1当たり量ですし、1クラス当たりの生徒数や針金1m当たり40円などというのも1当たり量です。 1当たり量は、いろいろな事柄を比較するときに便利な量です。 日本の小学校の学校規模は、1校当たり600人とか時には1校当たり1000人とかになっていて、大きいほうが競争があって子どもが伸びるというような神話がありますが、、諸外国では1校当たりの生徒数は200人以下で、諸外国の方が子どもたちに手厚い教育を行なっていることがすぐわかりますね。 行政は、このため、補助金などいろいろな事柄を、1当たり量で表すことを大変嫌っております。 そこで、国民は、補助金全体を人数分で割って、一人当たり分を出すというようなことをしなければならないことが多いのです。割り算は、国民が1当たり量を求めて比較するための武器になるのです。1当たり量は掛け算や割り算に関係している量で、足したり引いたりできません。 距離や時間がkmとか時間とか単位がひとつしかついていないのに対して、 1当たり量は、km/時間というような2つの単位がついているのが特徴です。その1当たり量を使うと、6×3=18は、例えば、こんなことを表していることになります。 カブトムシ1匹当たり足6本 で 3匹分 では 足は全体で18本 単位をつけて式をかくと 6本/匹 × 6本 =18本 練習問題 次の式は、どういうことを表していますか。上の例にならって、最初の数を1当たり量だと考えて、具体的にどんなことを表しているか考えてこたえてください。ア 2×3=6 ヒント 1当たり量が2のもの:(例)ヒヨコ1匹当たり足2本とか鳩1匹当たり羽2枚、人間1人当たり手が2本など 答え方 ヒヨコ1匹当たり足( )本で、( )匹分では、足は全体で( )本イ 4×5=20 1当たり量が4 のもの:ウ 8×2=16エ 1×5=5オ 0×4=0(オ)の問題を解くと、0をかけるとなぜ0になるかが分かります。私たちが小学校で学んだ 速度×時間=距離というのは、掛け算の代表的な構造をもっています。速度と時間と距離という異なる3つの量の関係を表しているからです。このうち、速度という量は、1当たり量であるのに対して、時間や距離は1あたり量ではありません。このように、じつは、量というものには、2種類あるのです。時間や距離は、 3時間+4時間=7時間 2km+3km=5kmというように足し算ができる量(加法性がある)ですが、速度は、 時速40km+時速50kmというような2つの車の速度を足すというような計算はそもそも意味がなく、できない(加法性がない)のです。さて、6×3=18という計算の中には、いちいち、6は1当たり量ですよとは書いてないのですから、私たち自身が、この掛け算を見たときに、「ああ、6は1当たり量を表しているのだな」ということを読み取らなくてはなりません。 このことがわかると、5、6年生になってきたときに 文章題がぐんととけるようになるでしょう。文章題がとけなくなるのは、掛け算とは九九のことだと思っていて、掛け算の大切な構造ということがわかっていないからなのです。文章題を見て、子どもがあせって、「かけるの、割るの」というようなことを聞くことがあるのも、それは、1当たり量という掛け算のなかに含まれている大切な量の見方ができていないことや掛け算の構造がわかっていないことにも原因があるのです。九九は暗記して使えても、掛け算は、本当は分かっていないのです。第2段階 プラスとマイナスは反対の性質を表す記号です反対の性質をもつことばはいろいろあります。上下、左右、東西、前後などです。いろいろな量も、反対の性質をもつ量があります。東方向に2kmと西方向に2kmは、ちょうど反対の量です。そこで東方向18kmを 東という言葉の代わりに+という記号で表せば+18km、西方向18kmは、西という言葉の代わりに-という記号で表せば-18kmとなります。同様にして、 東方向に時速6kmで走っている自転車は、+6km/時 西方向に時速6kmで走っている自転車は、-6km/時同様にして 今から3時間後を+3時間と表せば 今から3時間前はー3時間と表すことができますね。3つの量にそれぞれプラスとマイナスがあることがわかりましたか?こういうマイナスを含む3つの量の関係を次に考えてみましょう。第3段階 正負の規則は、こうして生まれる 速度と時間と距離という3つの量は、それぞれ正負の量があることは、前のところでふれました。では、速度×時間=距離 の関係を使って、正負の規則がどのようにして生まれてくるのか調べてみましょう。(1) 自転車に乗って、東に向かって時速6kmで走っています。今から3時間後には、現在地からみて、どこにいるでしょうか? これは簡単ですね。東方向18km地点です。これを、式に直すと、 (東方向6km/時)×(3時間後)=(東方向18km)正負の記号で表すと (+6km/時)×(+3時間)=(+18km)ここから、(+)×(+)=(+)という関係が出てきます。(2)自転車に乗って、西に向かって時速6kmで走っています。今から3時間後は、現在地からみて、どこにいるでしょうか? これは、(西方向)18km地点ですね。これを、式にあてはめると、 (西方向6km/時)×(3時間後)=(西方向18km)正負の記号で表すと (-6km/時)×(+3時間後)=(-18km)ここから、(-)×(+)=(-)という関係が出てきます。 (3)自転車に乗って、東に向かって時速6kmで走っています。今から3時間前は、現在地からみて、どこにいるでしょうか? これは、(西方向)18km地点ですね。これを、式にあてはめると、 (東方向6km/時)×(3時間前)=(西方向18km)正負の記号で表すと (+6km/時)×(ー3時間後)=(-18km)ここから、(+)×(ー)=(-) という関係が出てきます。(4)自転車に乗って、西に向かって時速6kmで走っています。今から3時間前は、現在地からみて、どこにいるでしょうか? さあ、これができれば、ゴールです。 これは、現在地点より(東方向)18km地点ですね。これを、式にあてはめると、 (西6km/時)×(3時間前)=(東方向18km) (-6km/時)×(-3時間後)=(+18km)ここから、(-)×(-)=(+) という関係が出てきます。 このように、速度や時間や距離という実在の量の関係から、正負の規則がちゃんと導くことができるのです。 規則として覚えるということと比べて、このようにして導かれたこの正負の規則は「なるほど」と生徒たちにも納得のいく規則として受け入れられるのです。 こういう勉強を私は、「本質が分かる授業とは?」ということで、大学で学生たちに講義してみたのです。こういう学び方ならば、子どもたちは、算数や数学を何のために学ぶのかがつかめて、学ぶことが楽しくなり、分かるようになって勉強するようになるのです。今日の正負の規則の説明が納得できた方は、下のマークをクリックしてくださいね。ご訪問有難う御座います。下の2つの教育ブログ・ランキングに参加しています。よろしかったら下のそれぞれのマークをクリックした下さい。ランクの点数が加算されます。人気blogランキングへ
July 30, 2007
コメント(2)
-

本質がわかる学びとは?塾等でバイトをしている大学生たちの感想
「本質が分かる学びとは」の授業を受けて(2) 塾の先生や家庭教師のバイトをしている大学生の感想とは?<個別指導の塾で教えているDさん。・・・無念でいっぱいです> 今日の授業は、目からウロコでした。すごく楽しかったです。すごく楽しかったです。 私は個別指導の塾で教えています。一次関数でつまづいてどうしても前に進めない子がいます。二学期の成績も下がってしまい、今月で退塾して、大手の集団塾へ移ることになってしまいました。 私は自分の力量のなさと教えることへの未熟さで無念でいっぱいです。 私は教科書中心で、教えることも下手だったと思います。もっと工夫して、分かる数学を教えてあげたかったです。もっともっと、教え方を勉強して、分かったよ!と言われるようにがんばりたいです。(Dさん)<家庭教師のEさん。・・・子どもたちは暗記することにかなりのストレスを持っている> 私は家庭教師のバイトをしているが、今日の授業内容をしっかりと頭に入れていれば、中学生が数学で苦しんでいるところのかなりの部分を解決できると思う。 子どもたちを見ていると暗記するということにかなりのストレスを持っていて、それでも学校は暗記することしか教えていないから、余計に頭に入らなくて苦しんでいる。 私も、実際、何をやっているのかわからないと覚えられない方だったので、今日学んだような生活に密着した学びをもっと勉強したい。(Eさん)<家庭教師で数学を教えていたFさん・・・因数分解に大変感心した> 先生が示された二次関数の因数分解は、大変関心させられた。以前、自分は家庭教師で数学を教えていたが、原理については無知だったため、生徒も自分も基本の部分で大分苦労した思い出がある。 ちょっとした工夫で、図や工作をすれば理解できるのだと改めて思った。(Fさん)ご訪問有難う御座います。下の2つの教育ブログ・ランキングに参加しています。よろしかったら下のそれぞれのマークをクリックした下さい。ランクの点数が加算されます。人気blogランキングへ
July 29, 2007
コメント(2)
-

今の子どもたちに必要なのはこれだ!(大学生Bさん)
「なんでこんなことやらなきゃならないの」という疑問にこたえる本質を大切にした学びを 前回、と前前回、一人の大学生Aさんの授業の「感想」についてとりあげましたが、「学習の目的を教えてほしかった」というAさんの要求は、本質がわかる授業を受けたときに、自分の知らない数学の世界を発見したことから生まれてきたものです。 こういう発見が何らかの形でなければ、「学校にたいする不満」の原因をつかめずに、それを心の中に沈殿させたままで、ずっと生きていくことになったに違いありません。 しかし、このような疑問は、決してAさんだけの問題ではないのです。 私がやった算数と数学に関する本質がわかる授業(2コマ)は、民間の研究団体の中では、もう何十年も前から知られている楽しくわかる算数・数学の教え方として定番のありふれたものをいくつか選んで紹介したものです。 ところが、そういう教えたかに、いわば受験競争の勝ち組に入った国立大学の教育学部の大学生たちがまったく出会わないで、小中高と過ごしてきているということを感想を読んで知り、愕然としました。 これは、教師が、教えられたようにしか教えていないという経験主義から学校が抜け出せないでいるということを示しているということを感じないわけにはいきません。 どうしてこうなるのかということがわかる、成り立ちやしくみがわかる、物事の本質が楽しくわかるという暗記やドリルをこえた授業は、子どもたちの根源的な要求だと私は考えているのですが、その要求は、そういうことがわかる授業に出会わないと子どもたちに自覚されないという性質をもっているように思われます。 小学校からそういう教育をきちんと受けていけば、中学や高校でも、もっと楽しくわかるように教えてほしいという要求は出てきて、教師の変革を求めるものになっていくのでしょうが、今は、そういう要求がでないために、あるいは受験競争や学力テストにかき消されて、教師に届くものになっていないのです。 10進法のしくみや分数の割り算のしくみ、因数分解の意味や三日月形のコマの重心を計算してまわすたった2コマ(1コマ90分)の授業を通して、このAさんと一緒に学んでいた学生たちもと、新しい世界を発見し、学ぶということの意味をつかみ、どういう教師になりたいかということまで考え出していきます。 次に、そういう学生たちの授業の感想を少しずつ紹介していくことにします。本質を学ぶことを大切にした授業とは・・・大学生の感想(1)<今の子どもたちに必要なのはこれだ> 私はもともと数学が好きなのですが、今日の授業を受けたら、やっぱり数学は楽しいなと感じた。久しぶりに数学の授業を受けた気がして懐かしかった。「学びたい」という気持ちが出てきて、今の子どもたちに必要なのはこれだ!っと思った。 なぜ勉強しなければならないのか? 生きていくうえで必要なことは学ばなくてはならないが、特に高校の数学でやるような難しい内容は、大人になったときに果たして使うのだろうかとずっと疑問だった。今回、関数が生活に役立つということを知り、うれしかった。(Bさん)<自分がいかに本質をわかっていないのに計算をしてきたかということを知った> 数学について、自分がいかに本質がわかっていないのに計算をしてきたか、ということを知りました。 そしてまた、自分が本質をわかっていないのに、子どもたちに教えるということは不可能であろうと思いました。 因数分解のしくみやブラックボックスなど、初めて目にしたものもあり、とても楽しかったです。これから学ぶこどもたちにも、このようなものを使い、本質がわかるように教えられたら良いのではないかと思いました。(Cさん)ご訪問有難う御座います。下の2つの教育ブログ・ランキングに参加しています。よろしかったら下のそれぞれのマークをクリックした下さい。ランクの点数が加算されます。人気blogランキングへ
July 28, 2007
コメント(3)
-

なんでこんなことやらなきゃならないの
「なんでこんなことやらなきゃならないの」という疑問は、なぜ起きてくるのだろうか。例えば高校の数学1で出てくる二次関数。そもそも何で二次関数をやらなければならないのか、教科書にも書かれていない。やることは、グラフ描きである。こういう疑問がわいてくるのも当然である。進学率90%を越える現代において、買い物さえできればいいと考える高校生も非常に多い。買い物するためには、四則演算さえできればいい、何で面倒くさい二次関数なんかやらなければならないのかという疑問がもくもくとわいてくる。受験科目にあるからということだけなのだろうか。こういう疑問がぶつけられたとき、暗記主義や反復練習主義(操作主義)で生徒たちの尻をたたいている教師は、よく、「やっておけば無駄にはならない、いつか役に立つ」とわかったようなことをいう。こうして、「何でこんなことやらなきゃならないの」という疑問は封印されてしまう。さて、それから何十年も過ぎて、大人たちは、二次関数なるものを学んでおいて、「先生の言った通り、無駄ではなかった、確かに役にたった」といえる人はどれぐらいいるのだろうか。子育てをしているお母さんにとってはどうであろうか。現代では、大学生は分数計算さえ忘れてしまうということが話題になっている。二次関数といえば、グラフ描きの練習しか思い出さない大人たちにとって、それは受験のためだけだったのだろうか。「なんでこんなことやらなきゃならないの」という疑問が出されたときは、じつは、教育のもっとも重要な場面なのだが、数学を大学に入ったときの専門的な学問の道具として考えていると、それはごく一部の人にしか通用しないために、「私は、文系に行くので使いません」などと言われれば説明ができなくなる。こうして、「なんでこんなことやらなきゃならないの」という疑問は、まともな回答を与えられないまま、小学生・中学生・高校生の心の中に沈殿していく。そもそも、二次関数よりもっと大切な学習内容はないのだろうか。二次関数より、指数関数の方が「なんでこんなことやらなきゃならないの」という疑問にははるかに答えやすいということはないのだろうか。子ども・若者たちが生きている現実と学習指導要領で決められた学習内容には、大きな乖離はないのだろうか。ご訪問有難う御座います。下の2つの教育ブログ・ランキングに参加しています。よろしかったら下のそれぞれのマークをクリックした下さい。ランクの点数が加算されます。人気blogランキングへ
July 27, 2007
コメント(5)
-

私の中の学校への不満
公式を覚えて数字をあてはめて計算する数学ではなく、本質がわかる数学を大切にしたいということで行なったある大学における授業の感想のひとつを紹介します。 高校以下の今日の学びをどう考えたらいいのかという点で、重要なヒントが示されているといえないだろうか。「何でこんなことやらなきゃいけないの?」・・・これがずっと私の学校への不満だった(Aさん) 今日の資料にも書いてあった「何でこんなことやらなきゃいけないの?」ということが、ずっと私の中での、学校への不満だった。 私はこれを数学にも感じていたが、英語に強く感じていた。そのおかげで、ずっと英語は苦手で、高校の頃も、今になっても大変苦労している。 なぜ、学ばなければいけないのかは、もうこの歳になったら自分で見つけ出さなければいけないのかもしれないが、せめて義務教育のうちは学習の目的などを教わりたかった。(U)ご訪問有難う御座います。下の2つの教育ブログ・ランキングに参加しています。よろしかったら下のそれぞれのマークをクリックした下さい。ランクの点数が加算されます。人気blogランキングへ
July 26, 2007
コメント(2)
-

『新・学力への挑戦』の実践はもう古くて現在の生徒には通用しないのではないか
先日、ある研究会で、拙著『新・学力への挑戦』に対して、次のような質問が出された。「この本に納められている実践は、80年代後半のものであり、その後、生徒たちも劇的に変化してきている。このような実践は、現在ではうまくいかないのではないか」というものであった。さて、拙著が取り上げている内容は、1975年以降の実践で広範囲にわたっているが、、特に1987年から3年間、1年、2年、3年と持ち上がりで担当した時の実践は最後の第7章でとりあげ、本書の重要な内容になってはいるが、その後の1990年から2000年3月に定年退職するまでの10年間の実践例を、現実の世界を批判的に読み解くメガネを手に入れる数学の学びとして、第1章(指数関数)と第2章(確率)で取り上げている。昨日書いた原発が大事故を起こす確率は、98年と99年の実践である。したがって、拙著はけっして80年代後半の実践とみなすことはできない。しかも、その後、2003年までの4年間、2つの大学において非常勤講師として、総合学習研究や教職概論等を担当する中で、高校以下の学力問題が大学生の中にどのように反映しているのかを研究する必要を感じてとりくんだ実践例も紹介している。したがって、拙著の内容は、過去のものではなく現在につながる内容をもっている。いや、むしろ、過去から一貫して取り組んできた本質を大切にするという角度からの授業づくりが、高校1年から3年まで、さらに大学生にまで通じるということにこそ、今、重要な関心を払ってもいいのではないだろうか。 私の取り組む授業の領域は、いろいろ変化したが、その核心には、いつも現在の競争の教育―暗記主義と操作主義に流され、点数や偏差値でしか学びをとらえられない日本の教育、学力問題に対する危機意識があったーに対して、もっと違う学び方があるではないか、学校は、各教科は、もっと本質を大切にした学びを太い軸にしていかなければならないのではないかと考えて取り組んできた。本質的なことは、現実の世界とかかわっていて、つながりあっていて、発展性があり、学ぶ意味と面白さを教えてくれるものであり、学ぶ意欲を与えてくれるものである。この間の生徒たちの変化はたしかに非常に大きいけれども、ある意味で、その変化に対応できる学びは、暗記主義や操作主義ではなく、本質を大切にする学びの充実というところにこそ解決の糸口あるのではないか。これらのことをふまえて、ここで簡単に実践の経過を整理すると、次のような関係になる(1)80年代前半までの高校3年の本質がわかる微積分の授業づくりの視点と方法が、その後、1,2年の数学1・2の授業づくりとしても有効であった。80年代後半、高校1年から3年までを持ち上がりで担当した授業づくりの実践(拙著第7章)はその具体的な事例となっている。(2)上記80年代後半の本質を大切にした授業づくりの視点と方法は、その後、90年代(~2000年3月)の授業づくりにおいても有効であった。(3)高校における本質を大切にした授業づくりの視点と方法は、2000年以降の大学の授業づくりでも有効であった。大学生たちは、本質を学ぶということの意味をはじめて知り、「目からウロコが落ちた」と感動した。(4)拙著『新・学力への挑戦』は、70年代後半から現在にいたるまで、一貫して本質をこそ大切にした学びの創造に取り組んできたささやかな実践記録であるが、今日、全国学力テストが実施され、足立区の不正事件に象徴されるようなおろかな競争にまきこまれた日本の教育において、改めて、学びの原点とは何かを教育に関心をもつすべての人たちに問いかけていきたいと考えている。ご訪問有難う御座います。下の2つの教育ブログ・ランキングに参加しています。よろしかったら下のそれぞれのマークをクリックした下さい。ランクの点数が加算されます。人気blogランキングへ
July 25, 2007
コメント(2)
-

恐ろしい動画を見た
今日のテレビで恐ろしい動画を見た。それは、新潟県中越沖地震発生時に柏崎刈羽原発3号機の使用済み核燃料プールの水が激しく揺れ、水がプール外のフロアにあふれ出る様子を撮影した動画で、東京電力が24日、公開したもの。3号機の燃料プールには、プルサーマルで使用するためのプルトニウムを含む混合酸化物燃料を保管。テロ対策の観点から、東電は6秒に1回の間隔で燃料プールを撮影するカメラを設置していたために記録されていたのだという。テレビの解説では、波立つ水は高さ1mにも達していたという。あふれ出た水はどこまで流出していたのか。例年だとにぎやかな柏崎の海辺は、今日は1組の親子だけが泳いでいるだけだった。今日は、このほか新たに6号機の原子炉建屋天井にある大型クレーンの移動用車軸2本が破断していたことを明らかになった。原発の安全性については、1975年当時から、例えば確率というひとつの学問を利用して、安全だと信じ込ませる学者たちがいた。米国原子力委員会は、1基の原発が1年間にチェルノブイリ級の大事故を起こす確率は、10億分の1だと主張していた。つまり、10億年に1回程度というきわめてまれなことだと言っていたのである。ところが、アメリカの科学者の中には、これはあまりにも小さすぎると1万分の1ぐらいはみなければならないと主張するグループがいた。米原子力委員会の仮説は、その後、チェルノブイリやスリーマイルの大事故によって、こなごなに吹き飛ばされた。私は、このふたつの仮説をもとにした世界中の原発が60年間に少なくとも1回大事故を起こす確率を計算して比較検討する高校数学1の授業を行なったことがある。(詳しくは、拙著『新・学力への挑戦』をご参照ください)ご訪問有難う御座います。下の2つの教育ブログ・ランキングに参加しています。よろしかったら下のそれぞれのマークをクリックした下さい。ランクの点数が加算されます。人気blogランキングへ
July 24, 2007
コメント(3)
-

安全神話が崩壊する
4月、北陸電力志賀原発第1号機(石川県)の「即発臨界」について書いてから、このブログは開店休業となり、もう3ヶ月以上がたってしまった。久しぶりにブログを書いてみようと思い始めたときに、中越沖地震がおき、刈羽原発の危険性が日ごとに明らかになってきた。原発の真下の活断層に気がつかなかったということだから、驚きだ。IAEAに検証してもらうことにしたらしいが、それは、原発の安全神話が国際的な基準から検証を受け、震度7の激震で崩壊するような日が近づいているということではないか。テレビで見ると、原発は柏崎の街並みにつながって見える。柏崎の人たちは生きた心地がしないのではないか。ご訪問有難う御座います。下の2つの教育ブログ・ランキングに参加しています。よろしかったら下のそれぞれのマークをクリックした下さい。ランクの点数が加算されます。人気blogランキングへ
July 23, 2007
コメント(3)
-

数学の学力とは?
「数学は何の役に立つのか」という問いに対して、私は、「現実の世界を批判的に読み解くために非常に役に立つ、そういう角度から、誰でもが数学を学ぶ必要性がある」と訴えてきた。 学力問題を「全国一斉学力テスト」などで競争させてるという動機づけで解決しようとするではなく、そのことを学ぶ必要性がわかるように学ぶことができるように、学習指導要領・教科書なども、その内容を根本的に見直すことが必要ではないか。私は、そのひとつの重要な視点として、数学で現実の世界を批判的に読み解くということを提起してきた。 詳しくは、拙著「「新・学力への挑戦」―数学で新しい世界と自分が見えてくるー第1章 倍々変化を読み解くメガネ、第2章「デタラメの世界を読み解くメガネ」をご参照ください。 昨日、「即発臨界」という新しい言葉が登場した。原発について、これまで「臨界」ということは、何度も聞いてきたが、「即発臨界」ということは知らなかった。 この間、次々に明るみに出てきた電力会社による過去の原発の事故隠しの中のひとつである。これは北陸電力志賀原発第1号機(石川県)の1999年6月18日の国による定期検査中におきた臨界事故である。 すでに、この事故は、「原子炉の制御棒が意図せずに3本抜け落ちて臨界状態が15分間続いた」と3月19日頃に大きく報道されてきたものだが、今回、日本原子力技術協会が、もっとも厳しい条件で分析すると、即発臨界になっていた可能性があるというもの。事故の2ヵ月後に志賀町などは2号機を受け入れている。また、3ヶ月後に、東海村の臨界事故が発生している。チェルノブイリ大事故は、この即発臨界をへて、水蒸気爆発にいたったといわれている。 原発の大事故を、生徒たちと確率を使って計算・予想すると、高校1年生が、これから50年間生きていく間に世界中に500基あると想定した原発の少なくともどれかひとつが大事故を起こす確率は、92%になるという計算結果が出てくる。この計算の根拠は、過去50年間にチェルノブイリとスリーマイルの原発の大事故という2回の大事故が起きているという統計的な確率をもとに計算している この統計的な確率から、1基の原発が大事故を起こす確率は1万分の1程度になるということがでてくるが、非常に小さく見えるこの確率で計算しても、50年間に世界中の原発の少なくともどれかひとつがチェルノブイリ級の大事故が起きる確率は92%にもなるという結果が出てくるもの。(詳しくは拙著第2章参照) 自分の計算結果が、地球と世界と自分の未来をどう考えたらいいのかという問題を高校生たちにつきつける。現実の世界を批判的に読み解くという学力とはこういうものである。「トイレのないマンション」といわれる原発の大事故の問題を数学的に考える授業をやってきた私にとっては、こういう一触即発の事故が、長年隠蔽されてきたことの恐ろしさをつくづく感じる。 「朝日」は、「北陸電力志賀原発第1号機(石川県)の臨界事故を受けて、日本原子力技術協会が当時の状況を解析したところ、最悪なら、急激な核反応が一気に起きる即発臨界になっていた可能性があることが11日わかった。即発臨界はチェルノブイリ事故でも起きた現象だが、志賀原発の場合は即発臨界が起きていたとしても、局所的なため、燃料の温度は損傷で危険な状態となるまでは、ほど遠かったと見ている。・・・」(朝日4/11)と伝えている。 原子炉の設計上は制御棒は1本抜けても臨界にならない状態しか想定していないということを私は知らなかったが、この事故は弁の操作の誤りで、その制御棒が3本も同時にぬけおちたことで臨界状態になったことが明らかになっていた。弁の操作は、経験のない電気関係の技術者が担当していたらしい。その制御棒の抜け落ちる速度や順番によっては最悪のシナリオとなり、即発臨界になっていた可能性があったということである。 「核分裂反応は、通常、温度が上昇すると減少する抑制効果がある。しかし、即発臨海だと、核分裂反応が減少することなく一気にすすんでしまう。燃料の温度が3300度をこえるような状態になると、核燃料が破損したり、水蒸気爆発を起こすおそれがあることから、起こしてはならない反応と考えられている」(同紙)という。 原発の安全性をいくら強調しても、こういう隠蔽があること自体、原発の安全性を国民に納得させることができないことを物語っている。 このような数学から導き出された結果をど読み取るのか、読み取る学力がどうなっているのかということは、上記拙著の中で、国立大学の教職を希望する大学生の計算結果に対する感想を紹介して考察しているが、それは、テスト学力がいかに深刻な破綻を引き起こしているかということを如実に示すものとなっている。テスト学力を求める競争の教育は、デタラメな世界にも法則があるという確率・科学そのものを受け入れることを拒否するまでになっている。(詳しくは拙著第2章参照)ご訪問有難う御座います。下の2つの教育ブログ・ランキングに参加しています。よろしかったら下のそれぞれのマークをクリックした下さい。ランクの点数が加算されます。人気blogランキングへ
April 12, 2007
コメント(2)
-

会津の少年時代(18)うつぼを仕掛ける
うつぼは、魚をとるための竹で編んだ細長い筒である。 中には、入り口から魚が入ると、出られないように折り返しがついている。 このうつぼの中に、炒った米ぬかに、みみずをまぜたものを布で包んで入れて、魚がその匂いにつられてうつぼの中に入ってくるように工夫する。みみずは隣の農家の台所のたれ流しのぐちゃぐちゃしたところにいくらでもいた。 うつぼの出口は、かわのそばの草をむしりとってまるめた草で栓をした。 夕方、夕日を見ながら田んぼのなかのあぜ道をあるき、魚のいそうな小さな川にうつぼをしかけていく。うつぼを3つ4つ持っていっただろうか。夜、魚たちは上流に向かうということから、うつぼの入り口は下流に向ける。 うつぼは、水の中に仕掛けても竹だからすぐ浮き上がろうとする。だから、すばやくあたりを見回して、適当な石を見つけ、それをうつぼの上にのせて沈める。だから、どこに仕掛けたのかわからなくなる。 そこで、道端に咲いているタンポポや草花などを折っては、仕掛けた位置に草花をおいて目印にしていく。 こうして、夕闇の迫った田植えの終わって蛙のなくた田園のなかを、そよ風に吹かれながら家路につく。竹は水に浮くということも、その浮力の大きさも、こういう遊びを通して、まわりの適当な重さの石を探すことを通して、当たり前のように自然のうちに学びとっていく。 1970年代だろうか、大学生が4本足のにわとりを描いたということが話題になったことが思い出されるが、もうそれから久しい。最近では、マグロといえば、「刺身が海を泳いでいる」と思っている子どもたちもいるという話を聞いたことがあるが、自然とまるごとふれあうのではなく、ごく一部の断片しか生活の中では見えていない。 今の子どもたちには、自然の面白さを自分が経験したように、体験させてあげたいと私は思う。自然を知ることは、こういう時間に追われない子ども時代の遊びを通して、自然の中でいろいろと失敗をくりかえし、試行錯誤しながらそれに働きかけて、とらえられていくものではないだろうか。 「教育再生会議」は、自分たちを任命した人たちが、かってにはじめた「ゆとり教育」を、今度は槍玉にあげて、夏休みまで減らすというようなおろかな提言をする?らしい。子どもたちが、豊に遊ぶということをどれだけ奪ってきたかということにまるで気づいていない。 まるで、「マグロの刺身が海で泳いでいる」と考えている子どもと変わらない。「テスト学力が社会を泳いでいる」わけではないのだ。子どもたちの発達ということの中味を本当に知らない人たちである。こうして、本当の意味での学力の危機は、何一つ解決されないままであるだけでなく、さらに深刻な問題になっていくだろう。 それは、政府や財界が期待するごくごく一部のエリートたちの創造性さえ奪う恐ろしい危機が進行していくということではないだろうか。おろかなことである。 さて、閑話休題。翌朝、仕掛けたうつぼが、誰かに荒らされたら困るので、夜が明けきらないうちに目を覚まし、寝床から抜け出して、家を飛び出す。まだ朝の空気は気持ちよく冷たい。 昨日、仕掛けた道順をたどりながら、目印を見つけてはうつぼをあげていく。どきどきする一瞬である。小川から引き上げたうつぼの竹の網目から水がざあざあと流れ出ていく。 水がぬけたら、出口につめた草を抜き取り、中をのぞき、逆さにして中のものを道に出す。小鮒はピンピンとはね、どじょうはにょろにょろと這い出す。大きいどじょうはでかどじょうがとれたといって喜んだ。バケツに入れてつぎの仕掛けたポイントに、目印の草花を探しながら歩いていく。 ご訪問有難う御座います。下の2つの教育ブログ・ランキングに参加しています。よろしかったら下のそれぞれのマークをクリックした下さい。ランクの点数が加算されます。人気blogランキングへ
March 18, 2007
コメント(0)
-

犬山の子は 犬山で育てる
「犬山の子は犬山で育てる」 第3章のタイトルである。 全国学力テストに参加しないことを決めた犬山市のとりくみをまとめた本が緊急出版されるというメールをもらった。その本のチラシが添付してあった。 先日、私は、犬山のとりくみを「すごいことだ」と書いたけれども、これだけのことを決めていくそのプロセスもぜひ学んでおきたいと思う。 会津育ちの私は、会津の少年時代をこれまで書いてきたが、本当に、その土地がらを生かした教育こそ大切なのだと思う。方言のもつことばとしての情感の豊かさなどもそのひとつだ。 「犬山の子は、犬山で育てる」という犬山市教育委員会の見識は、本当に立派なものだ。 競争VS学びあい・・・日本の学力問題の本当の解決の筋道を,人間関係を切り裂く競争で刺激しないと解決できないと考えている文部科学省に対して、人間関係を豊かにしていく学びあいという方法もあるのだということを犬山市は示しているようだ。 全国一斉学力テストは、子どもたちのストレスを強め、相次ぐいじめ問題をさらに深刻にしていくことも十分予想される。 いのちの大切さを説く文部科学省が、子どもたちを危機に追い込むようなことをしていいのだろうか。私は、犬山市の教育委員会がその自主性を大事にしたとりくみから学びたい。ご訪問有難う御座います。下の2つの教育ブログ・ランキングに参加しています。よろしかったら下のそれぞれのマークをクリックした下さい。ランクの点数が加算されます。人気blogランキングへ
March 16, 2007
コメント(0)
-

会津の少年時代(17) ザルで鮒を取る
小川に出かけて魚とりをするときは、昔は、台所にある深いザルをちょっと借用して出かけたものである。 ザルで魚を取るには、川草の下手にザルをおき、片手で押さえながら足をじゃぼじゃぼいわせて魚を追い立ててザルの中に追い込んでいく。 頃合をみはからって、ザルをあげると、竹で編んだザルいっぱいに水が入っていて重いけれども、ザルのすきまから水がザアザアと出ていくようにザルをぐーるぐーるとまわす。水がだんだん少なくなってザルの底が見えるようになってきたとき、鮒がかかっていれば、鮒がザルの底でピンピンはねて暴れまわる。これがワクワクするほど楽しい。 腰が痛くなってくるまでそうやって川の中を歩いては、魚のいそうな場所を見つけて魚をとり続けた。辛抱強さは、子どもたちを夢中にひきつけるこういう面白い遊びを心ゆくまでする間にいつの間にかできていったように思われる。 とってきた鮒やどじょうは、今度は、家の裏に小さな池などを掘って、水を張りそこに入れて遊んだりした。 ご訪問有難う御座います。下の2つの教育ブログ・ランキングに参加しています。よろしかったら下のそれぞれのマークをクリックした下さい。ランクの点数が加算されます。人気blogランキングへ
March 14, 2007
コメント(1)
-

「全国学力テスト」は、象の尻尾の長さで象を論じるようなもの
国は4月には、「全国学力テスト」を実施すると意気込んでいるようだが、推進している人たちは、そこで測れることがどれだけ限定されたことかということを想像する学力というものを欠落させている。学力テストで測れることはごくごくわずかであることを知るべきである。全国学力テストは、象の尻尾の長さで象を論じるようなものである。 例えば、私は、ここ数回、記憶の彼方になりつつある会津の早春の思い出を書いてみた。書きながら自然の恵みを豊かに与えられた自分の少年時代が髣髴とよみがえってきた。そういう少年時代をもつことができたことを感謝するとともに、今日の環境破壊ということへの怒りが、自ずから生まれてくる自分がいることにも気がつく。環境破壊の悲しさと悔しさを理解する豊かな環境ということの意味を自然からたっぷりと教えられてきたからである。ものごとはそういう関連の中で深く理解できることである。 そして、現在、豊かな自然に恵まれた少年時代をもてたということ自体が、年をとった一人の人間の生を内面から限りなく支える力、生きる豊かな力になっていることを感じる。 テストで、「『早春』という漢字を書きなさい」という問題が出れば、漢字自体は書き方を練習し、覚えて書くことはできる。ただ、書き方の練習からは、早春というふたつの漢字の中にこめられている豊かな内実というものは生まれてこない。 しかし、「『早春』ということばから、どんなことを思い出しますか。具体的に書いてください」という問題が出たらどうだろうか。ふたつの漢字を前にして、子どもたちはどんなことを思い出し、想像し、胸をときめかせて書くことができるのだろうか。都会の子どもと山村の子どもとどちらが豊かな内容を書くことができるだろうか。 単純な漢字テストの成績としては、都会の方が高い結果が出るだろう。しかし、生活の中で、空気の冷たさも、風のやわらかさも、草花の芽吹きも、小川の流れの勢いも、眼に移るものすべてが、耳に聞こえるすべてのものが、ただよう芳しい香りすべてが、手を切るような水の冷たさが、冬から春への季節の美しい変わり目を、いきいきと教えてくれている山村の子どもたちの方が断然書きたい内容をもっているのではないだろうか。 そのことを引き出す設問になっていないだけである。形式的・抽象的・操作的な力だけを測るようなテスト結果をどれだけ統計的に処理して全国比較し、市内の小学校ごとに比べても、グラフなどに視覚化したとしても、それは学力というもののごくごく限られた一面をあらわしているに過ぎない。だから、象の尻尾の長さで象を論じるようなものである。 東京でも品川区をはじめ独自の学力テストを行い、その結果を公開して、小学校にまで序列をつけるというおろかなことをしてきた。尻尾だけならば、象より大きな動物たちもいっぱいいるのである。 そんな右ならえの時代に、愛知県犬山市の教育委員会が、4月24日に実施されるという全国学力テストに、全国でただひとつ不参加を決めたという。私は、いろいろ圧力もあるだろうに、すごいことだなあと感心している。 ご訪問有難う御座います。下の2つの教育ブログ・ランキングに参加しています。よろしかったら下のそれぞれのマークをクリックした下さい。ランクの点数が加算されます。人気blogランキングへ
March 10, 2007
コメント(3)
-

会津の少年時代(16)早春のどじょう取り
朝昼夕と蒸気機関車は、サケノ坂を上り始めるときに、ピョオーという汽笛を鳴らした。村人たちはこの汽笛を聞いて、どこにいても今何時ごろか見当がついた。毎朝、会津若松へ通学する高校生たちは、上りと下りが交換する上三寄駅へと急いだ。会津若松から、田島方面へと西から東へのびていた会津日光街道沿いに、大戸村は家並みをならべていたが、線路もこの街道沿いに伸びていた。 会津日光街道と線路で、村は北側と南側に二分されていた。家並みを少しはずれると、北側にも南側にも田んぼが広がっていた。その田んぼのあぜ道の間に、緑の草に覆われたような幅が30~40センチほどの無数の小川が走っていた。 これらの小川は、田んぼに水を供給するのに欠かすことの出来ない水路であったが、当時はフナやどじょうやめだかなどがいっぱいいて、子どもたちの格好の遊び場だった。 雪が解けはじめた早春の魚とりは、この田んぼの小川でのどじょうとりから始まった。魚とりといえば、網や台所の笊を持ち出したりして使うのがふつうだったが、早春のどじょうとりは、スコップをかついで出かけた。 この時期は、まだ、水が流れていない小川があった。そういう川では、どじょうたちは土にもぐって冬眠でもしているらしい。どじょう取りは、いきなりやわらかな川底にスコップを突き立て、川底の泥を一気にすくいあげてあぜ道に放り投げるというやり方である。 そうすると、泥の中でいい気持ちで寝ていたどじょうたちがびっくりして目をさましにょろにょろと出てくるのである。これがおもしろい。 水の中に住んでいるとばかり思ったどじょうたちは、冬のあいだ、水のなくなった川底の泥の中でちゃんと生きていたことがわかるのである。 子どもたちは笑い転げながら、まだ、風が冷たい早春の田んぼの中の小川で、夢中になってスコップで泥をすくい上げては、どじょうを取った。ご訪問有難う御座います。下の2つの教育ブログ・ランキングに参加しています。よろしかったら下のそれぞれのマークをクリックした下さい。ランクの点数が加算されます。人気blogランキングへ
March 9, 2007
コメント(1)
全189件 (189件中 1-50件目)