全1730件 (1730件中 1-50件目)
-
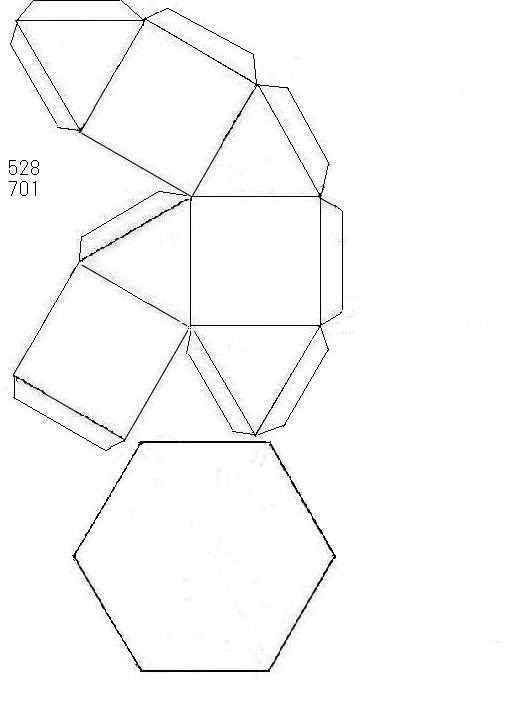
三角台展開図
前ページで三角台についての補充をしましたが、このページでの三角台の画像を投稿するに際して、急遽、正方形と正三角形をそれぞれ3枚作って、それを展開図のようにコピー紙に貼つけて組み立てました。 多面体紙工作の古い設計図を見ていたらその展開図を設計したのがあったので、下に載せます。台の底面は、用紙の都合で別に切り取り、貼り付けることにしました。 画中の数字は画像サイズで、コピーするとき(変更するときなど)同じサイズになるように、ピクセル数を記入しておくのです。
Sep 15, 2016
コメント(0)
-

三角台テトラポッド
三角台を基礎にした多面体を作りました。三角台を4個、底面を合わせてテトラポッドとしました。これは見る角度を変えると立方体の部分が見えます。光ってる面は三角台の斜面の正方形が二面、同一平面になっている面です。更に、これを拡張したテトラポッドを作りました。正三角形が見える角度を表示します。 正三角錐が3個あるので、この部分の延長線が正三角形になっています。このように基礎のものをいろいろと変化させると変わった多面体が出来るのが面白いのです。多面体の種類は多いので、このようにオリジナルの多面体が出来て嬉しくなります。三角台について補足説明を致します。台板が正三角形であるので、三角台と呼びます。台ですから、横板が支持板になっていて、正三角形3枚と正方形3枚で構成されています。多面体の一種ですから、面数を見ると、それは天板が一面と横板が6面、そして底面が一面の合計8面で、8面体になります。画像を表示します。紙工作品ですので貼り合わせが上手ではありませんので、辺の接続がピッタリとは行ってません。ボール紙で切り取った正三角形3枚と正方形3枚を正三角形の周りに、コピー用紙を台紙にして、貼り付けて組み立てました。底面はそれに合わせて、正六角形面を貼り合わせました。上の画像では底面が見えていません。古い日記を見ていたら、既に投稿したのがあった。下記のページです。Dec 28, 2012 楽天プロフィール XML 三角錐追加した三角台四面体の星型多面体を創りました (1) こちらのほうが写真画像が綺麗に表示されています。「もっと見る」で、カテゴリー全表示のページにはいったら、「数学」をクリックします。若い時のほうがしっかりと投稿できたのだなと老齢を感じます。もう一度、古い投稿のページを見ていたら、このページの補足になるような記事がありましたので、追加します。Dec 27, 2012 楽天プロフィール XML 正六角四面体に三角台を載せて膨らませたら立方体が見えてきたこの記事の中の「正六角四面体」はその画像では実在しません。中は空洞です。三角台の底面4枚を合わせて構成されていると仮想したので「正六角四面体」と記入したのでした。2日、連続して同じ作品について投稿していたのでした。理解を深めて頂くためと考えていたのかもしれません。現在の感想です。
Sep 13, 2016
コメント(0)
-

複合多面体もオイラーの定理が適用できます
正六面体正八面体複合星型多面体にもオイラーの 定理が適合することを見てゆきます。青い色紙を貼った立方体はわかりますが、金色の噴霧塗装を施した正八面体は、この画像では認めにくい。大きな正三角形が二面見えるが、隠れているのが六面有るのです。それぞれの面に立方体の角(頂点)が表出しています。 正八面体の正三角形が4面見える画像を下に表示します。立方体の一面が見えています。 先ず、面と頂点と辺の数を調べます。 面の数 正六面体 3×8=24 、正八面体 4×6=24 合計48 頂点の数 正六面体 8 、正八面体 6 コル 12 も頂点と数えます。 これらの合計は26 青と金色の角錐の接点がコル(鞍部)です。これも頂点です。 辺の数 正6面体 3×8=24 、 正8面体 4×6=24 これらは 1/2 の大きさの辺を数えている。 さらに正6面体と正8面体の同一面(面上)にある辺も数える。 正6面体の面上で数えると 4×6=24 (同じ辺を正8面体の面上で数えると 3×8=24 どちらの面上で数えても、同じ数になる) ここで 面と頂点と辺の数を整理すると、 面 48 頂点 26 辺 72 オイラーの定理は 線の数 = 頂点の数 + 面の数 - 2 72 = 26 + 48 - 2 で 適合する これで、 星型多面体(特に、複合星形多面体)にも オイラーの 定理が適合することが判明した。ちなみに、2012年12月25日の日記(数学)にも同じ表題で6種類の星形多面体をオイラーの定理が適用出来ることを書いています。
Sep 8, 2016
コメント(0)
-

凸型540面体
正三角形の面で出来るだけ多くの多面体を作ることを考えた。もう、既にいくつも作っているが、最近また、3個作った。サッカーボール(正五角形12面、正六角形20面)正三角錐を載せた立体です。その個数振り分けは正五角形面 5✕3✕12=180正六角形面 6✕3✕20=360 合計 540サッカーボールの面 正5角形 12 正6角形 20
Sep 7, 2016
コメント(0)
-

マグネットスィッチと光センサー
標題のような電子回路を作りました。下図のような装置です。光センサーに光を照射させて、発光ダイオードが赤く光っている画像です。開閉回路の上に磁石が乗っていますので、マグネットスウィッチはONに成っています。
May 3, 2015
コメント(0)
-

正方形と正六角形と正八角形で立体を作る
ただし、正八角形は穴開きになっています。これは、ジョンソンの立体 s10 を はがき大の画用紙で作ることです。 これを 正方形と正六角形の組み合わせで、正八角形が穴になるように設計して、作りました。 s10 画像です。印刷するパターンは 実線はきります。破線は折り曲げる。その部分が貼り合わせる場所になります。これらを組み合わせて(貼り合わせて)正八角形の穴開きの立体が出来上がります。 貼りあわせた画像は 展開図 に成ります。画像で分かるように、正方形と正六角形が必ず隣り合わせに、貼り合わせられていますので、作り方の説明は、全く必要ありません。この作り方のメリットは、正八角形が穴に成って開いていますので、貼り合せの時、其処へ指を入れられる事です。そのため、貼り合わせがしっかりと出来ます。そして、数学的には、4、6、8 の辺で作られた面の組み合わせで出来ていることが、大変興味がわきます。4 6 8 は公差が2の等差数列になっています。これらの面が、それぞれ、何個で出来ているか数えるのも、面白いと思います。 帰省した息子に、「これを上げる」と言ったら、「前にいくつも貰っているからいらない」と返答されたので、「じゃ、幾面体だか、数えてみろ!」と言ったら、持ち帰って行った。
Oct 6, 2014
コメント(0)
-

手作り買い物袋
矩形の布で作られた一風換わった買い物袋を発見した。 これを調べてみたら、正方形が3連に成った矩形で作られていることが分かった。縫い合わせるところが2箇所。下図の通り。 OPは山折 2箇所 そして、Aの辺を縫い合わせる。同じく、Bの辺も縫い合わせる。縫い合わせる時の順序がある。最初にAを縫い合わせられるように、左側のOP線を山折にする。次に、Bが縫い合わせられるように、右側のOPの線を山折にする。が、縫い合わせる2枚の中に、最初に折った面が入っているので、これを一緒に縫わないように注意する。その注意は、この中の正方形面を対角線で折って、Bの辺と重ならないようにする。言葉だけではこの実態が理解できないが、上の方法通りに作ってみれば容易に理解できる。 そして、買い物袋にするには、α点とω点を両手で引っ張れば、最初の画像のような袋が出来上がる。これを考えた人は、トポロジーの名人だと思った。そのように感心したのであった。これを書くきっかけになったのは、ある観光地の土産屋で風呂敷に2枚のプラスチックハンドルをつけて手提げ袋が出来るのを売っているのをテレビで見て、どのように風呂敷を折って、ハンドルをどのようにつけるのかと考えたが、判明できなかったとき、このテーマの買い物袋を見つけたので、それを解明したのだった。 いづれ、その風呂敷の手提げ袋の解明が出来るのでないかと希望を持っている。(その風呂敷を買えば、折り方や作り方の説明書も付いていると発言していた。その店は鎌倉駅の前)
Jul 23, 2014
コメント(0)
-

漢数字だけで表現した和歌の石碑
不思議な漢数字だけの和歌家の中の整理をしていたら、こんなものが出てきました。平成7年6月のカレンダーの裏にメモされたものです。それには縦書きに粗雑に記録されたメモでしたが、その大元の文字を列記します。 八万三千八 三六九三三四七 一八二 四五十三二四六 百四億四百漢数字だけで表現された和歌ですが、何と詠むのでしょうか。 平成7年の初夏に碓氷峠下りを歩いたことがあったのですが、その時通った熊野神社の近くにあった石碑に刻まれていたものです。それはこのように読むのだそうです。 山道は寒く寂しな 一つ家に 夜毎身に染む 百夜置く霜 当時メモした紙にそのように書いてありました。カナ書きを意味の分かる表現に書き表したものです。 メモの画像を載せる
May 7, 2014
コメント(0)
-

1円硬貨600個と5円硬貨80個で銀行に預金してきました
「両替をしてからでは手数料がかかります」と案内の人に教えられたので、預金票に必要事項を記入して、番号札で呼び出されるのを待った。 やがて呼び出されたので、1円硬貨を100枚ごとにまとめた仮の袋を4袋と、5円硬貨が20枚づつまとめられた袋2袋を、指定された黄色いプラスチックの箱2つに、ざらざらと、それぞれを入れた。やがて、計数されて、「4円足りません」と言われたので、4円をがま口から出した。 帰宅して、袋を捨てようと思い、その前に袋の中に残っていないかと見たら、2つの袋から、1円が出てきた。結局、数え間違いは、千円のうち、2円だけだった。この沢山集まった千円は、預金が出来たのだった。でも、こんなに多く、よく、集めたものだと、感心した。硬貨のカウントに当たって、下図のようなゲージを作った。 二つのブロックで、各1枚ずつ足りなかったのは、ゲージに満杯に入ったつもりでも、入っていなかったのだと思う。6回のカウントに対して、2回だけ1枚少なく計数されたのは、やはり、正確なゲージでなかったと言うことがいえる。 紙工作の好きな男にとって、1円玉を600枚数えたり、5円玉を80枚、いちいち数えるより、このゲージを作って計測するほうが、らくだと考えたので、それを実行したのです。簡単に1000円が計測できたので気楽に終わった。 「4円足りないです」と言われたのは、そういうこともあるだろうと考えて、1円硬貨を余分に持って行ったのだった。
Apr 22, 2014
コメント(1)
-
EXCEL の前身Microsoft Multiplan の値段 68000円
古い雑誌を整理していたら、ASCII 1988年3月号の資料請求ページに Microsoft Multiplan 3.1 NECPC-9800シリーズ対応 価格68,000円と言うのが目に入った。 昔はずい分高価なソフトだったのだなあと気がついた。このマルチプランと言うのはEXCELの前身であって、現在はMicrosoft Office になって、word やそのたいくつかのアプリケーションソフトプログラムが含まれていて数万円で使用できる。EXCELだけでなく、その他 OneNote Outlook PowerPoint Publisher Word などが含まれている。 これだけの豊富なソフトが含まれていて、現在は4万円足らずで使用できる。(普通は購入すると言っているが、開発者は使用を許可すると言っているので、使用できると言う表現になる。) 26年前は、こんなに高価なソフトだったのだと気がついた。その高価なソフトを使用していたと思うと、ずいぶん高額な金額を払わせられていたのだと思う。PCが普及すると、ソフトは非常に安くなると言うことである。
Apr 10, 2014
コメント(0)
-

群馬県高崎市にも大雪
ラジオの報道では、前橋が31cmとありましたが、高崎ではそれよりも多く積もった.
Feb 9, 2014
コメント(1)
-
完全数に対する不足数と言う考え方
8192は完全数であるか? 不足数についての例14個の数列を項h比を2とした数列で考えてみる。終りの項は8192となる。この8192は完全数であるか8192の約数の数列は、下のようになる。1 2 4 8 16 32 64 128 256 512 1024 2048 4096 (8192)完全数であることの条件は、n-1個(自分自身を含まない個数)の約数の数列の和が自分自身と等しい時の数である。自分自身を除いた約数の数列の和は1+2+4+8+16+32+64+128+256+512+1024+2048=8191この8191は8192(自分自身)より小さい数である。つまり、8192に対して不足しているので、不足数となる。注不足数の定義については、下記のような記述がある。(ウィキペディアによる記述)この不足数の定義は「その数自身を除く正の約数の総和が元の数より小さくなるような数」と同値である。例えば「15の自身を除く約数の総和は 1+3+5=9
Oct 22, 2013
コメント(0)
-

サンシュユの赤い実 と 碓氷川の濁流
春は黄色い葉が夏には緑の葉になり、秋には赤い実が実ります。その赤い実をデジカメ撮影に行ってきました。木の生えている場所は鼻高山です。鼻高展望花の丘に隣接した南斜面に群集して植林した樹林があります。 小さな赤い実ですが、その量たるや見事なものです。帰りに碓氷川を覗いたら茶色の濁流が勢いよく流れていました。昨夜の雨の名残です。
Oct 16, 2013
コメント(1)
-

繁茂した柿ノ木
毎朝涼しいうちに庭の手入れをしている。雑草除去が終わって、次は木の手入れを行おうと考えた。 柿ノ木は伐採した時のまま放置してあったので、今は葉が多く茂っている。木を伐採したのは何時だったろうかと、ブログの前のほうを検索したら、2011年10月29日にそのことが記載してある。しかし、画像が3枚とも表出されていない。これを再現する。その1枚目が丸坊主になった画像がある。楽天写真館に登録したのはちゃんと立ち木になっていたが、写真館では、このように横倒しにされている。首をかしげて見てください。丸坊主の様子がおわかりでしょう! さて、今朝撮影した画像は、ご覧の通り繁茂しています。生命力のものすごさに感服する。今年は実が全くつかないと思っていたが、木の葉の中をよく見上げてみたら、大きな実が5個成っていた。 天地宇宙を創造した神はこのような柿木も大きく育てていてくださる。柿の大好きな妻は今年は実がならないと、がっかりしていたのだが、「5個成っているよ!」と教えたら、大喜びだった。妻は、買い物に出ると、必ずといってよいほど柿を買ってきて食べている。この大きな柿の実5個は落下しないで実っていて欲しい。食べられるようになるまで木に着いていてください、と祈る気持ちで眺めた。この気持ちは私の妻に対する愛情です。2011年10月29日のブログにも、画像を再現しましたので、そちらも見てください。
Oct 2, 2013
コメント(0)
-
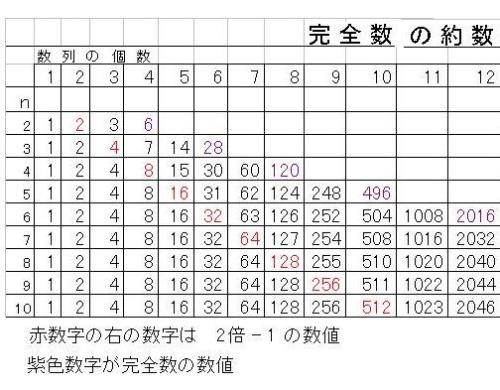
完全数の約数表を大きく表示して数字がはっきりと見えるようにしました
この数表を大きく表示したいとので、表を分割して載せました。この表の右側の図を下に載せます。大きな表が表示できて、その数字の羅列がたいへん美しく感ぜられます。赤数字と紫数字の色区別藻はっきりと認められて、規則正しく数字が並んでいるのが、本当に奇妙なくらい不思議で、驚かされます。だから、完全数!?表の見方1 最左の縦列の数は紫数字の完全数まで数列の半数(紫数字は約数ではない) 完全数の公式のnをあらわしている。2 最上部の横列数は、その数列の個数3 左側のn個と右側のn個は左から右へ2倍となっている。4 赤数字の右の数字は(赤数字×2-1)ここが不思議な点です。 しかし、間違いなく約数です。 以上の特徴が非常に綺麗に整っているのが美しい!ここではn=10までとしたが、上の特徴を考慮すれば、nは20でも、30でも完全数が求められるはずです。 初めてこの完全数を発見した人は30数個までしか求められていないと、あるコーナーに書いてありました。 コンピュータがなくて、手計算だったからでしょう。 なんとしても、ぜひともこの数の並びの美しさを見てもらいたかったので、こんな工夫をして大きな数字の見易い表に作り直しました。
Sep 23, 2013
コメント(0)
-
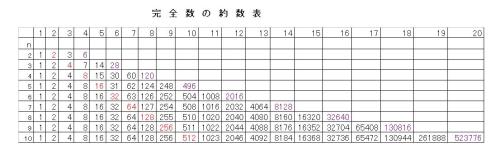
神様がお作りになった完全数
神様がお作りになった完全数 天地創造をなさった神様が、数の管理統制もしておられると信じる。それであればこそ、このように不思議な数も神様には簡単に作られる。それを発見した人は、神を証明したのです。数学の分野において。あまりにもすばらしい数であるので、その完全数の表を、もう一度作り直しました。見やすいように、罫線も引きました。完全数を含めた2n個の数列の中央で二倍系列が変わるn個目の数を赤数字で表現しました。一番右の完全数は紫数字で表現しました。EXCELで作った表ですが、元図はA4判の紙に一杯になるようにして非常に見やすい表でしたが、楽天写真館では、この種の表は大きく表示してくれないようです。どこかクラウドにでも、大きな表を載せましょう。(少し時間を下さい)表の見方1 最左の縦列の数は紫数字の完全数までの約数の個数(紫数字は約数ではない)2 最上部の─列数は、その数列の個数3 左側のn個と右側のn個は左から右へ2倍となっている。4 赤数字の右の数字は(赤数字×2-1)ここが不思議な点です。5 nは完全数公式のnでもある。 以上の特徴が非常に綺麗に整っているのが美しい!ここではn=10までとしたが、上の特徴を考慮すれば、nは20でも、30でも完全数が求められるはずです。 初めてkの完全数を発見した人は30数個までしか求められていないと、あるコーナーに書いてありました。 コンピュータがなくて、手計算だったからでしょう。
Sep 22, 2013
コメント(0)
-

完全数が与えられた時、nを求めるマクロプログラム」
EXCEL2000でマクロプログラムを作って、nを求めてみました。下の数表は 完全数32640をA1セルに書きこんで、マクロ実行した結果です。 A1 とC2が等しくなって、nの値は8になっています。そのプログラムを下に載せます。 Sub FORN()Call NumberSet サブルーチンを呼び込むEnd Sub 以下がサブルーチンです。Sub NumberSet()Range("A1") = "32640" ・・・・ A1セルに完全数を書き込む.Range("A2").Formula = "2"Range("D1").Formula = "1"Range("C2").Formula = "0"Do Until Range("C2") = Range("A1") 等しくなるまで繰り返す Range("B1").Formula = "=A1/2" Range("A1").Select 循環参照エラー防止策で2行セットする Activesel1 = "" Range("A1").Formula = Range("B1") Range("b1") = Range("a1") 元の数値に戻すため Range("B1").Select 循環参照防止策 Activesel2 = "" Range("C1").Formula = "=A2*2" Range("A2").Select Activesel1 = "" Range("A2").Formula = Range("C1") Range("c1").Formula = Range("a2") 元にもどすためのステートメント Range("C2").Formula = "=C1-1" Range("D2").Formula = "=D1+1" Range("D1").Select Activesel1 = "" Range("D1") = Range("D2") Range("D2") = Range("D1") ・・・・ D1セルに n の値が表示されている.LoopRange("d3").Value = "nの値"MsgBox "nの値は" & Range("d1") & "です"End Sub此の設計に先駆けて、完全数は120として、プログラムを作った。繰り返しの検証が楽であることを考えたのです。エラーが何度も出て、そのつどマクロの参考書と首引きでステートメントを書き換えては実行して、デバッグを行った。 苦労もしたがエクセルのマクロを楽しんで、マクロの図書をもう一度読み直す機会を得た事は幸いだった。 何十年もプログラムを作らないでいると、その作法を忘れてしまうものですね。
Sep 19, 2013
コメント(0)
-

表記が困難だったので省略した計算式
指数式と対数式の表記が面倒であったので省略したが、JPG画像で表記すると下図の様になる。
Sep 19, 2013
コメント(0)
-
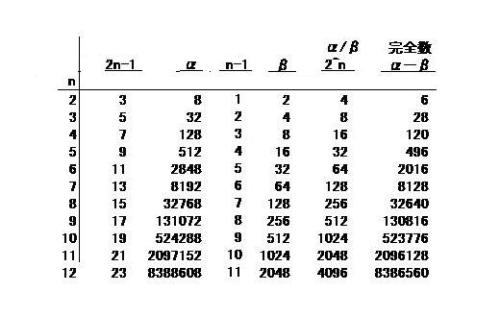
完全数公式の指数と対数の関係
完全数公式の指数と対数の関係完全数の公式は 2^(n-1)(2^n-1)=2^(2n-1)-2^(n-1)これを 2^(2n-1)=α・・・・・・(1) 2^(n-1)=β・・・・・・(2) 故に 完全数は α-β で表せる。 上の(1)式と(2)式を 対数形式で表して、操作してみるとそれぞれ、次式のようになって、その結果が面白い。 計算式は省略します。 計算結果は 2^n = α/β が現れる。これらの関係を表に作ってみた。 perfect number table3.JPG
Sep 17, 2013
コメント(0)
-
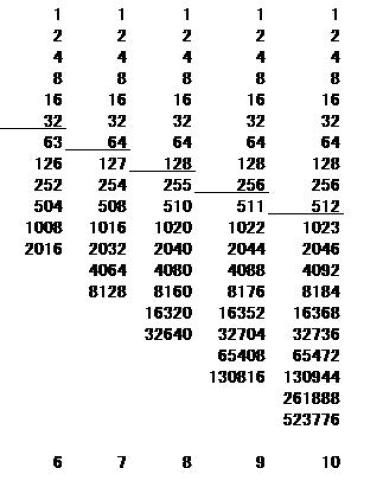
完全数に関する問題
完全数に関する問題完全数に関してまとめのつもりで、その問題点を考えてみた。問題1 完全数が与えられた時、その約数を列挙する。問題2 その約数の個数を数えること問題3 その約数の最大値を挙げること。問題4 その完全数を求める式において、nはいくつか。これらを調べる時、次の2個の数表が役立つ。表1 perfect number 6-10 ・・・9月11日ブログの表と同じ 完全数の約数表の n=6 から n=10 までの約数と完全数の一覧表です。 下線の有る数字までは上から順次2倍した数が列挙されている。 下線の有る数字の次の(その下の)数字は2倍した数マイナス1の数です。 以下は順次その数の2倍した数となっている。 一番下の数字 6,7,8,9,10 は 下線数字までの約数の個数で、完全数を求める公式のnと一致している。 縦数列の一番下の数が完全数です。表2 perfect number table2 表1を横書きにした表です。約数の数列が見られます。その数列の右側の最大値が完全数です。一番上の行は個数を示す数です。一番左の縦列は完全数を求める式のnの値です。約数の最大値 完全数の 1/2 の数 これは完全数の一つ左側にある数問題1から問題3までは上の二つの表から、簡単に求めめられるが、問題4を完全数の公式から計算で求めることは非常に困難であった。かなりの時間を費やして計算を試みたが、答えは出なかったので、これもまた、表にしてみることにした。 その方法は完全数を求める公式から 完全数は α-Β として考える表としたのでした。 此の表については、次回の記載と致します。
Sep 16, 2013
コメント(0)
-
等比数列の公式を用いて証明する
等比数列の公式を用いて証明する完全数 n=4 のときの 完全数を求める数列の和が 2^3 + 2^4 + 2^5 + 2^6 を求めることとなったので、等比数列の公式を用いて解いてみる。等比数列の公式は Sn=a*(1-r^n)/(1-r) ただし r ≠ 1 初項 a 、項比 r、項数 n上の式に於いて a=2^3 、r=2 、n=4これらを公式に当てはめると Sn=2^3*(1-2^4)/(1-2)=(2^3*-2^3*2^4)/(1-2) =2^3*2^4 - 2^3 = 2^3(2^4 - 1)以上で 2^3 + 2^4 + 2^5 + 2^6 は 2^3(2^4 - 1) であることが証明された。 公式も忘れてしまって、それなりに、昨日は解いてきたが、公式を用いれば、このようにスマートな証明が出来たのでした。(簡単な計算でした。)
Sep 13, 2013
コメント(0)
-
メルセンヌ素数による完全数公式の証明
メルセンヌ素数による完全数公式の証明 Mn=2^(n-1) であれば、完全数は 2^(n-1)Mn=2^(n-1)*(2^n-1)で求められる。この式が成立することを約数の合計から求めた式で、証明する。n=3 のとき 1 + 2 + 4 + 7 + 14 = 28 = 2^0 + 2^1 + (2^3 - 1) + (2^4-2) = 2^0 + 2^1 + 2^3 - 1 + 2^4 - 2 = 2^2 + 2^3 + 2^4 = 2^2 + 2^2 * 2 + 2^2 * 4 = 2^2 * (1 + 2 + 4 ) = 2^2 * ( 7 ) このとき 7 = 8 - 1 = 2^3 - 1 であるから 28 = 2^2 * ( 2^3 - 1) = 2^(3-1) * (2^3 - 1) 結果は 2^(n-1)Mn=2^(n-1)*(2^n-1) を満足している。同様に n=4 の時も 120 = 2^3 + 2^4 + 2^5 + 2^6 = 2^3 * (1 + 2 + 4 + 8) = 2^3 * 15 = 2^3 *(2^4 - 1) n=5 のとき 496 = 2^4 * (1 + 2 + 4 + 8 + 16) = 2^4 * 31 = 2^4 * (2^5 - 1) n=6 のとき 2016 = 2^5 * (1 + 2 + 8 + 16 + 32) = 2^5 * 63 = 2^5 * (2^6 - 1) n = 7 , 8 , 9 , 10 と 代えても、同様に 完全数を求める公式で計算したのと同じ結果が求められる。 以上の結果でわかったことは、約数の数列の和を表計算で行ったのと公式で求めたのと合致するということです。
Sep 12, 2013
コメント(0)
-
メルセンヌ素数による完全数
メルセンヌ素数による完全数 Mn(=M^n-1)のメルセンヌ素数を用いて完全数が次の式で求められる。 2^(n-1)Mn=2^(n-1)(2^n-1) 注 : ^ は べき乗上式によって完全数は次に示されるように求められている。(n を 2、3、4、.....9、10と代える) 6=2^(2-1)(2^2-1) 28=2^(3-1)(2^3-1) 120=2^(4-1)(2^4-1) 496=2^(5-1)(2^5-1) 2016=2^(6-1)(2^6-1) 8128=2^(7-1)(2^7-1) 32640=2^(8-1)(2^8-1) 130816=2^(9-1)(2^9-1) 523776=2^(10-1)(2^10-1)これは表計算で求めた数値と一致する。nは数表では自分自身と約数の個数の合計の半分の数値と一致しているのが面白い。 数表でn=4に該当する完全数120の数列の合計からメルセンヌ素数を用いた完全数の式が導き出されることが証明も出来る。次回は此の証明を記載します。
Sep 12, 2013
コメント(0)
-

数表計算で求めた完全数
数表計算で求めた完全数前頁で、数列個数の半数値が7~10までの完全数も、同様に表計算で求められると信じたので、それを実行した。下の図のように求められた。約数表示の一番下の数値が完全数です。(この数値は約数には該当しない)自分自身と約数の合計個数の半分の数値が、次のページ(9月12日記載)に記述してあるメルセンヌぬ素数のnと一致している。 n=6 のとき 2016 n=7 のとき 8128 n=8 のとき 32640 n=9 のとき 130816 n=10 のとき 523776完全数を除いた上表の約数(2n-1個)の合計が完全数である。nは上の表の最下部の数値です。
Sep 11, 2013
コメント(0)
-

二倍より一つ少ない関係で成立している完全数の不思議さ
神の作られた完全数は全く不思議な数である。このことについては、1月6日の日記に書いたが、この数をダウド・サットンは、更に続けて説明している。次のとおり。 新ピタゴラス学派は、最初の完全数が 6 なのは「神が6日間で世界を創造した」こと(天地創造)、次の完全数が 28 なのは「月の公転周期が28日である。」と。月の公転も、地球の自転も、すべて神の御手の内に有る。 この完全数も神が作られた数であり、それを数学者が発見しただけのことである。しかし、人間が考えた時、全く不思議な気がする。この約数の数列を見たとき、すべて、一致した規則がある事を発見してまさに驚いたのです。この数列は丁度中間が2倍数の関係を逸して居るだけで、凡て2倍数になっている。 下の表はそれを示している。最上部の数が完全数である。自分の数(完全数)を除いた数列の和が完全数と呼ばれたものであって、自分を含めた数列の個数の 1/2 を最下部の線外に記入してある。 この数列の中央線の上の数は下の数の2倍より1だけ少ない。この線の上側も下側も、上の数/下の数=2 が成立する。6個の完全数をこのような規則で作られているのを発見して、これ以上の大きな完全数も、同じ規則で作られていると想像した。「想像した」と言ったのはそれ以上の表計算をしてないからであって、多分、同じ規則になっていると信じたのであった。 ここ数ヶ月、ブログの記入がなかったのは、宇宙天地、世界を創造された神のことを瞑想していたのであって、1月16日に認識させられた完全数のことについては、以上の事は全く知らずにいたのでした。 ブログの記入もだいぶご無沙汰したので、何か書かなければならないと考えた時、この完全数の不思議さを発見したのであった。 科学者は、結局は神の栄光をあらわす仕事をしていると言うのも新しく発見したことでした。 そして、多面体成るものも、神が既に作られてあったもので、それを私は熱心に製作し、その中の数学を楽しんでいたのは、神が私に与えてくださった趣味であると同時に、そのことから神の栄光を顕すと言うことなのであった。多面体は「アートオブゴッド」(art of GOD)であると、私は信じたのでした。この完全数についても、多面体研究を行ってきた時に、知ったのだから。
Sep 10, 2013
コメント(0)
-
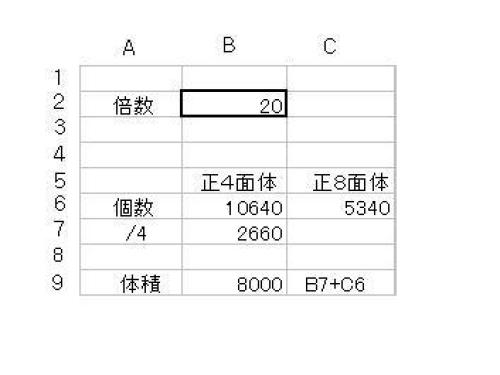
表計算は便利_たちどころに求める数値が出る_正8面体拡大
正8面体の個数 Sn8 = (1/3) * n(n+1)(2n+1) - n^2正4面体の個数 Sn4=(1/3)*4n(n-1)(n+1)上の計算を行うのに、nを入力すると直ちにSn8とSn4を表示してくれるプログラムを、表計算で行おうと考えた。その結果下のような書き込みをセルにセットした。セルB2に拡大する倍数を入力すると、たちどころに、それぞれの個数が表示される。上図では倍数20をセルB2に書き込んだ。セルには下記のように書き込みがなされてある。B6 =4*B2*(B2-1)*(B2+1)/3 C6 =B2*(B2+1)*(2*B2+1)/3-B2*B2 セルB6には正4面体の個数が表示され、セルC6には正8面体の個数が表示される。この計算表は、非常にコンパクトに作られた。表計算は たいへん便利です。
May 7, 2013
コメント(1)
-
辺の大きさをn倍にする正8面体を合成する正8面体と正4面体の個数を求める
正8面体と正4面体の合成で、辺の大きさをn倍にする正8面体を作るときの関連公式(1) 正8面体の個数n^2の数列の総和を求める式は Sn=1^2 + 2^2 + 3^2 + ・・・ + n^2 = (1/6) * n(n+1)(2n+1)で あるから その必要個数Sn8は Sn8 = 2Sn -n^2その結果、次の式が求められる。 Sn8 = 2 * (1/6) * n(n+1)(2n+1) - n^2 Sn8 = (1/3) * n(n+1)(2n+1) - n^2(2) 正4面体の個数表計算で求めるとき、各セルに2m*(m+1)をセットしたが辺の大きさを5倍にするときの例で、公式を作ることを解明する。各セルには 下記のように セットされている。 1層 2 * 1^2 + 2 * 1 2層 2 * 2^2 + 2 * 2 3層 2 * 3^2 + 2 * 3 4層 2 * 4^2 + 2 * 4 5層 2 * 4^2 + 2 * 4 6層 2 * 3^2 + 2 * 3 7層 2 * 2^2 + 2 * 2 8層 2 * 1^2 + 2 * 1 上記 の 全合計Sn4は Sn4 = 2 (1^2 + 2^2 + 3^2 + 4^2)*2 + 2(1+2+3+4)*2 =4{(1/6)*4(4+1)(2*4+1) + (1/2)* 4(4+1)}一般に m層までの全合計 Sn4 は Sn4=4{(1/6)*m(m+1)(2m+1) + (1/2)*m(m+1)}辺の大きさをn倍するとき、mはnより一つ少ない数値であるから m=n-1 を 上式に代入して、(中間計算式は省略する)正4面体の個数 Sn4 は 次の結果を得る。 Sn4=(1/3)*4n(n-1)(n+1)総合結果 辺の大きさが等しい正8面体と正4面体を合成させて辺の大きさがn倍になる正8面体を作るとき、必要個数は下記の計算式で求められる。正8面体の個数 Sn8 = (1/3) * n(n+1)(2n+1) - n^2正4面体の個数 Sn4=(1/3)*4n(n-1)(n+1)公式の適用4月24日に表計算で求めた20倍の正8面体を作るときの正8面体と正4面体の個数を求めてみよう。正8面体の個数 (1/3)×20×21×41-20×20=20×7×41-400=5740-400 =5340正4面体の個数 (1/3)×4×20×19×21=4×20×19×7=10640 この結果は4月21日に表計算で求めた結果と等しい。この結果は表計算を使わなくても、公式から簡単に求められるということだ。
May 6, 2013
コメント(0)
-

ケプラーの星型8面体の体積に関連して面白い発見あり
ケプラーの星型8面体は正8面体の各面に正4面体を載せたのと同じ立体であるので、正8面体の体積と正4面体の体積が分かれば、その合成により求められる。辺の大きさをaとして正8面体の体積 (√2/3)a^3 ( a^3 は aの3乗とする)正4面体の体積 (√2/12)a^3同じ辺の大きさで比較して正8面体の体積はは正4面体の体積の4倍である。以上のことから、ケプラーの星型8面体の体積は √2a^3 であることが分かる。ケプラーの星型8面体の頂点を直線で結ぶと正6面体(立方体)が形成されるのでその立方体の12箇所の削り取られた部分を立方体の体積から差し引けば、ケプラーの星型8面体の体積が求められる。こんな求め方は、普通は、しないが 数学的には興味がある。 この方法で求めるには、その削り取られた部分の体積を知らねばならない。これは、下図の4面体の体積を求めると、不思議なことに正4面体の体積と同じ結果が出る。 上の図で、ABDCの立体は、立方体から削り取られた4面体をコピー用紙で作り、埋め合わせた様子を表示している。(ADの長さは√2a OCの長さ=OBの長さ=(√2/2)a )逆に、立方体の体積からケプラーの星型8面体の体積を引くと、削り取られた12箇所の4面体の体積の合計が算出される。その1/12が正4面体の体積と同じ数値になっている。これに関連した実験を Aug.30.2011 に行っている。「違った形の多面体の体積が等しいことを砂で実験する」として、記事を書いている。そのときに実験器具に使った多面体が、下図のようなものであった。この右図が正8面体の1/4のものであって、これを4個合わせると正8面体が合成されることが発見されて、ケプラーの星型8面体は不思議な立体であると感慨深く感じた。 以上のことは、実際に計算して確かめたのであるが、計算式の羅列は一般の読者には不要の長物と考えて省略します。この計算結果で、いちばん驚いた不思議なことは削り取られた4面体と正4面体の体積が等しいことだった。数式計算に興味のある人は、ぜひとも、以上の計算を行ってみてください。不思議な結果が、実感できますヨ!不思議な計算吟味0 立方体の体積 (√2a)^3=2√2a^31 削り取られた4面体の体積2 立方体からケプラーの星型8面体を差し引く、体積計算3 立方体から削り取った12箇所の4面体合計を差し引く、体積計算 すべて、想定したとおりの結果が出ます。
Apr 29, 2013
コメント(0)
-
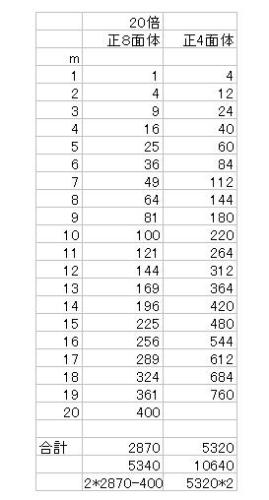
正8面体の拡大合成 20倍では正8面体と正4面体はそれぞれ何個になるか
正8面体の拡大合成 20倍では正8面体と正4面体はそれぞれ何個になるか前頁で、20倍でも30倍でも、発見された一般式に基づいて計算すれば簡単に求められると書いたので、実際に計算してみる。EXCELでの表計算では、正8面体5340個と正4面体10640個で合成できることが分かった。 その表計算結果は下記の通り。 ただし20倍だけを計算する。この計算の合理性の確証正4面体個数を正8面体に換算する。10640/4=2660正8面体の個数は合計で8000個(5340+2660)となる。20倍にしたので、体積比は20の3乗に比例するので、8000となる。これが正8面体の総個数8000個という数値8000に等しくなるので、表計算して求めたそれぞれの個数は 正8面体 5340個 正4面体 10640個この個数は正しいと証明された。正8面体合成に関する隠された規則的な数式を発見したことによって、EXCELによる表計算が簡単に出来て、合成に要する2種の多面体の個数が簡単に求められるようになった。これは数学の遊びであって、実際に正8面体を5340個と正4面体を10640個作って、大きな正8面体を合成するなどという根気の要る作業はまったく出来ないのが実情だ。先に、20倍でも30倍でも簡単に求められると発言したので、その実証をしたまでのことである。
Apr 24, 2013
コメント(0)
-
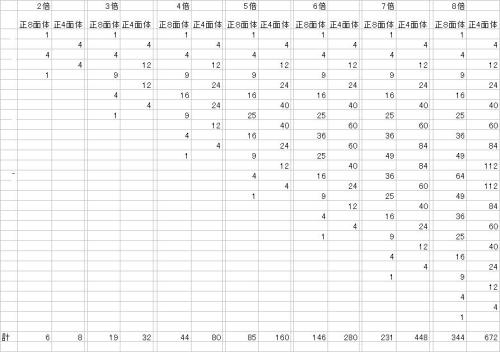
正8面体の中に隠された不思議な規則性のある数式
正8面体の中に隠された不思議な規則性のある数式 正8面体の辺を4倍にした正8面体で実験したので、この正8面体でそのことを見て行こう。逆に正8面体の辺を四分の一の大きさの正8面体と正4面体が中に何個含まれているかということを考える。その答えは正8面体が44個と正4面体が80個含まれているということになる。 先ずこの答えが正しいことを証明しておこう。正4面体は体積が正8面体の四分の一であるので、この80個の正8面体は20個の正8面体に相当する。この大きい正8面体の中には正8面体が64個(44+20=64)あると考える。この64個の正8面体の体積は辺の大きさの3乗に比例するので、4の3乗が64となって、公式通り正しいことが分かる。正8面体の個数を計算するときの数式の規則性正8面体が4階層になっている1,4,9,16はそれぞれ階層数の2乗となっていて、小さな正8面体階層数までのそれぞれの階層数の二乗となっている。正8面体の個数を計算するときの数式の規則性は二乗という簡単な規則であることが分かった。正4面体の個数を計算するときの数式の規則性この場合の正4面体の階層は3である。この数値は辺の比(4:1)の4からマイナスの3である。 第1表から辺の比がいくつであっても、その階層数は辺の比マイナス1なのである。 さて、今見ている正4面体の3階層の数値は4、12、24である。この数値の規則性を見出そう。 4=1×4 =1×2×2 12=2×6=2×2×3 24=3×8=3×2×4階層数をmとすると、m×2×(m+1)と成っているので、各階層の数式は 2m(m+1)であらわせる。辺の大きさが1である正8面体をn倍にしたときのこの正8面体の中に含まれる正4面体の個数を計算するとき、n-1階層までの数値を、この数式に当てはめて設定して、その合計の2倍が正4面体の個数である。辺の大きさをn倍にしたときの正8面体と正4面体の個数計算 nはいくつであろうと、以上の数式を用いれば、表計算によって、簡単に計算して求められる。 第1表 拡大に要する正8面体と正4面体の個数表第1表は辺の大きさを8倍にしたときまでの表であるが、10倍であろうが、20倍であろうがどんな倍数でも表計算で計算ができる。その数式を用いた表計算の合理性 第2表 拡大に要する個数表表計算によって得られた正8面体と正4面体の個数の表が倍数の3乗になっていることが証明されたので、第1表は正しいことが分かる。 この第1表を作るとき、不思議な規則性の数式が発見されたので、表計算が容易に出来たのであった。
Apr 16, 2013
コメント(0)
-

8面体と正4面体を組み合わせて大きな正8面体を作る問題_正8面体と正4面体それぞれの個数計算
8面体と正4面体を組み合わせて大きな正8面体を作る問題_正8面体と正4面体それぞれの個数計算 この計算は非常にややこしいのですが、大変興味ある問題ですので、発表します。過去において、正四面体の拡大についての個数計算問題を解きましたが、それ以上に面倒な問題となっていました。 何しろ多面体模型を紙工作で行って、それを積み上げていって確証したのでしたから。今回はその正四面体よりも個数を要する手間のかかる問題となりました。とても7倍までの確証実験は行いきれません。しかし、数式が発見されれば、7倍どころか9倍でも10倍でも、正八面体の拡大に要する正8面体と正4面体のそれぞれの必要個数が計算できることが分かったのでした。その実験を行った3倍拡大と4倍拡大の実験から見ていただきます。正8面体と正4面体で変の大きさを3 倍にした正8面体を組み立てる 3倍拡大組み立てるとき、正8面体と正4面体を積み上げられるように、正8面体の形状に合うような入れ物を用意した。その入れ物に2種類の正多面体を組み合わせて、辺の大きさが3倍になるような正8面体が合成された。正8面体が19個、正4面体が32個で合成されている。組立順序正8面体と正4面体で辺の大きさを4 倍にした正8面体を組み立てる 4倍拡大正8面体が44個、正4面体が80個で合成されている。実際に正8面体を44個と正4面体を80個作り、用意した入れ物の中に組み込んで行ってその個数を確認した。その合成正8面体の写真です。 4倍合成手順下から入れ物の縁まで積み上げた図は省略されて、正4面体24個の辺が入れ物の縁と同じ高さになった図から示しています。1 がその図です。2 は その次に正8面体を16個を載せた図です。3 は その上に正4面体を24個を載せた図です。この組立順を表にしたのを次に示します。 4倍_組立順序表 最初に正8面体を1個いれ、次に正4面体を4個入れることを赤の矢印で示している。最後に、正8面体を1個載せれば終わりです。それでは、辺の大きさを5倍、6倍、7倍などと 大きくして行ったら 正8面体と正4面体の個数は幾つになるのだろうか。これを計算で求めてみたのが、次の表です。 拡大に要する個数表この表は、次の表を個数の合計数をまとめた表ですが、下の組立表の合計だけを表にしたものです。 拡大に要する正8面体と正4面体の個数表この表を作るにあたって、計算式を求めました。その計算式は、どのような構成になっているかを考えて、正8面体と正4面体の構成数式が次のように発見されました。正8面体についての構成式 二乗の式 4、9、16 は 2の二乗、3の二乗、4の二乗 です。正4面体についての構成式 は 各倍数の正4面体を順次入れた順で、表にしてみたとき、その構成が発見されました。その正4面体個数計算表を下に掲げます。 正4面体個数計算表この表は正4面体の下半分の個数表です。したがって、正4面体の合計個数はその2倍になります。この計算を行うに際して、EXCELで表計算を行いました。倍数をmとすると、セルに入る数式が 2m(m+1)に成っていますので、セルには m*2*(m+1)と書き込んであります。mは倍数を示すセルです。このようにして、合計計算もΣで簡単に求められた。2m(m+1)の式を発見するにあたっての数値の整頓を行って、どんな構成になっているかを考えてみたら、どのセルも同じ構成になっていることがわかったのです。その発見過程についての説明は、次回のページで致します。
Apr 13, 2013
コメント(0)
-

正20面体 と ダ・ヴィンチの星_第5番目の星(自由な製作)
正20面体正20面体作品どの頂点にも正三角面が5個集まっている。5個集まった正3角形の輪郭は正5角形になっているのが特徴。貼り合わせが楽に出来る正20面体の展開図ダヴィンチの星 第5番目の星 正三角錐が5個集まっているのが見える。1個を見るだけでなく、数個置いて違った角度から見るのと同じ見方が出来るので、作品を4個並べて写した。自由に製作できる組立部品の設計図 この正三角形が直列に並んだ帯で正3角錐を作り、その組み立て方で自由にダ・ヴィンチの星が自由に作れる。いろいろな組み立て方をして、創造性を発揮させるのが楽しい工作となる。四個組の正三角錐と二個組の正三角錐の集合正3角錐が4個の部品が二つ(正3角錐8個)、正3角錐が2個の部品が六つ(正3角錐12個)で、合計20個の正3角錐がある。これらを自由に組み合わせて、ダ・ヴィンチの星を作る。 正20面体の特徴を理解しているので、正5角錐が5個集まるように組み合わせてゆく。自由な発想で組み合わせるので、時には、1個を切り離さなければならない場合が生しる。その場合の準備で、接続用の糊代部品が用意されている。 決められた通りに組み立てるだけでは面白みが無いので、こんな部品で製作するのが創造性をたくましくするのに役立つ。
Apr 12, 2013
コメント(0)
-

正12面体 と ダ・ヴィンチの星
正12面体 と ダ・ヴィンチの星正12面体古葉書で作る正12面体用紙の使用率を考えると、部品組立のほうが大きな立体が作れる。展開図法で作ったのと大きさを比較してみる。 左が部品組立法で作った正12面体 右が展開図法で作った正12面体 その設計図を下に提示する。 4分割した部品で組み立てる設計図 ダ・ヴィンチの星 第4番目の星 作品部品組立て法による設計図貼り合わせと組立途中の作品噴霧塗装のかからないように糊代を折り込んで隠して吹きかけた。乾燥してから糊代を正規に折り返したが、一箇所そのようになってないところがある。 設計図面の実線と破線の表現 実線は山折、破線は谷折であるが、実線だけでも折込が分かりやすいときは、破線は用いない場合が多い。製図が楽に出来る方法とする。
Apr 10, 2013
コメント(0)
-

正8面体とダヴィンチの星
正8面体正8面体は割合簡単に作れます。ダイレクトメールなどの葉書で、購入しない場合には、この用紙がよく用いられます。そのようにして作った正8面体が噴霧塗装をするのを待っています。上右図ダ・ビンチの星 第3番目の星部品図から製作するのでなく、変わった展開図で製作しようと考えて、以下のような設計をいたしました。 創造性を逞逞しくした設計です。糊代が取れ無い所は糊代を特別に同じ用紙で準備してあります。別の糊代は6箇所。谷折と山折を間違えなければ、正確なダビンチの星が作れます。要点は正3角錐を作ることです。 この別糊代を5箇所で済ませるようにしたのが次の設計図です。作品部品組立法による設計図(1)2部品で組み立てる(2)4部品で組み立てる (1)も(2)も、どちらも正3角錐が4個連なって、その開いた断面が正方形に成っている形の2部品を貼りあわせることで完成する。 その際、正方形の面がピッタリと合うようにする工夫がある。それは糊代の下側に糊代がへこまないようにする枠を貼り付けておく方法です。
Apr 6, 2013
コメント(0)
-

正6面体とダヴィンチの星
正6面体とその正方形の6面に正4角錐を6個載せたダ・ヴィンチの星左図が正6面体で右図がダ・ヴィンチの星です。2番目の星です。ダ・ビンチの星 製作部品図外郭を切る回数を減らすために、赤線で描いた部分は接触している。底の無い正4角錐を6個作り、それを貼り合わせて24面体を作る。 正4角錐を2個接続した部品図 部品図に糊代が必要以上に多くあるので、その糊代をどのように利用するか考えながら作るので楽しみが倍加する。
Apr 3, 2013
コメント(0)
-

正4面体とダ・ヴィンチの星
正4面体 正4面体が多量に作られた画像を展示します。正4面体に正4面体を4個載せたダ・ヴィンチの星単色の画像では全体の形がどのようになっているか分かりにくいので、載せた正4面体に色紙を貼り、それをさまざまな方向から写真に撮りました。 このだ・ヴィンチの星は簡単に作れるので、大きさも変えたりしてたくさん作りましたので、それを展示します。製作展開図実線は山折で、破線は谷折にして、糊代部で貼り付けて出来上がる。
Apr 3, 2013
コメント(1)
-

正8面体と正4面体の合成で正4面体を拡大する_6個の多面体で正8面体を作るパズル
正8面体と正4面体の合成で正4面体を拡大する_6個の多面体で正8面体を作るパズル 正4面体と正8面体で作る正8面体の拡大 以前、正4面体の拡大については記述済であるが、正8面体の拡大については記述してなかったので、この度、新たに正確な設計を起こして、その確証を記述することとした。 以前の作品の画像 これは正8面体の隣接正三角面に正4面体を二個載せて出来た合成多面体4個と正8面体2個で組み立てられている。 正8面体の隣接正三角面に正4面体を二個載せて出来た合成多面体の設計図 その設計図を画用紙に印刷してデジカメで撮影した画像この設計図で製作した8面体4個と正八面体2個で辺が2倍の正8面体が組み立てられる。その合成多面体の体積計算をしてみると当然のことであるが、興味ある計算が行える。正4面体の体積を1として計算する計算表を下記に示す。辺が2倍になると体積は8倍(2の3乗倍)に成る。上の計算表は正4面体の体積を1としたときの表であるので、32/4=8 が辺を2倍にした正8面体の体積比となって、計算は正解となる。 立体の体積は体積比の3乗に比例するというのが、この表で認められている。数値を見るのは面倒だ、興味が無いという人にはつまらない冗長な計算だと思われるが、「多面体紙工作で数学を楽しむ」というのがこのことなのです。関連ページ 2009年 6月11日 正8面体に正4面体を4個あわせると、辺が2倍の正4面体となる2009年 6月21日 正4面体と正8面体の組合せで、大きな正4面体を作る 日記一覧のページを開くリンク我楽免機の日記の一覧 多面体紙工作での実験A B C D は 正8面体に正4面体が2個載っている形の8面体 E と F は 正8面体 左図は正8面体を置いた図 右図は8面体を2個 合わせた図左図は8面体を1個だけ追加して合わせた図 右図は更に8面体を1個合わせた図最後に正8面体を載せて辺が2倍の正8面体が完成した図「この6個の多面体で、正8面体を作りなさい。」と言うパズルを行なおうとも考えたのであった。更に、部品を多くして(8面体を二等分した、正4角錐と正4面体の合成多面体8個にする)「8面体8個と正4面体2個との合計10個で、せい8面体を作れ」というパズルも作れる。8面体を2等分した設計図
Mar 29, 2013
コメント(0)
-

天神山登山で出遭った植物たち
3月26日天神山で出遭った植物たち山の花連魚_ツツジ若葉登山道を遮った倒木 前ページに載せた画像と同じものですが、倒木は植物ですので再度載せました。台風で倒れたものでしょうが、あちこちに倒木があって、道を遮っていたのはこの倒木だけでした。赤松空を見上げたら、松ポックリがたくさん着いているので面白く感じたので撮りました。葉がまったく無いので、枯れ木のようです。しかし倒れずに空中に鎮座しているという感じです。スミレや犬のフグリやホトケノザなど小花が当たり一面に咲いていて、風は冷たくても春を感じた山登りでした。
Mar 28, 2013
コメント(0)
-

天神山登山道
温室_コーヒーカフェ ここが登山口です山道 歩き出して直進して、左に曲がりやがて右に曲がったら、この倒木に出遭った。この下を、膝を着いて歩を進めて潜り抜けた。痛い膝が更に痛く感じた。その後は、難なく山道を進んで頂上まで上りあげた。グルコンEX錠を7ヶ月飲み続けて、ようやく階段が普通に近い常態で上り下りできるようになったので登山道の歩行も出来るのでないかと試験をしたのだった。歩き方はのろいが、背が高いので、大股で杖をつきながら割合楽に歩けた。普通山歩きは小またで歩くことが多いが、膝を痛めた後の予後を心配してゆっくりと大股で歩くことを考えたのです。お休み処山頂まで100m急斜面を登る旧登山道を表示しています。この旧道が参道でした。山頂まで約100m舗装道路には成っていませんが、新しく造られた山頂直下の近道です。表示近所の山ですので、気軽に登れる山であったから、楽しいしばらくぶりの登山が出来た。しかし、春とは言えまだ風が冷たくほほを打ちます。頂上は日向簿おっ子をしなければ寒いくらいに強い風が吹いていた。3月26日の日中の登山でした。
Mar 26, 2013
コメント(0)
-

t天神山頂上にての撮影
午前10時半 快晴。 バイクで天神山登山口へ行く。頂上での撮影結果のみを、このページに投稿する。あずまやパラグライダー離陸場三角点天神山_318m三角点の近傍の樹木に板が架かってある。石大きな火山岩がテーブルにしつらえてあり、その周りに石が椅子として置いてある。山頂での赤城山眺望花曇りであるので、赤城山がうっすらとしか見えない。山の植物や登山道の様子は、次のページに投稿する。
Mar 26, 2013
コメント(0)
-

高崎クリスマスローズガーデン
すばらしいガーデンがありますので紹介します。富久樹園と名前がついていますが、現在はクリスマスローズが最盛期ですので、その案内といたします。 国道406号を高崎市内を里美(榛名町)まで行って、県道132号で左折して安中市方面に行きます。この県道は高崎市と安中市の境である峠がに向かって昇り坂道になっています。ゴルフ練習場や榛名山の絶景を見ながら車を走らせると、峠近く左側に、クリスマスガーデンの看板がありますので、その道を左に入ってヘアピンを曲がれば、山桜と榛名山の絶景に当たります。ちょっと休憩して、此処に車を止めて、尾根の方を見れば、紅梅と白梅の林が見事です。 尾根伝いの農道を直進すれば、やがて右手に、目的地のガーデンに到達します。 この後の案内は写真で見てもらいます。 コーヒーカフェ天神山登山道準備中クリスマスローズクリスマスローズ2コウムコウム2カフェ内部カフェテラスからの眺望温室 駐車場の隣に大きな温室が有ります。水沢山_サクラ帰りは、東側の道を下るとき、この景色にあたります。
Mar 22, 2013
コメント(1)
-

突然_一斉に花が咲きました
昨日までは蕾だったのが、今朝は一斉に花が開いていました。水仙家のコンクリート基礎近くの水仙の花です。毎年、このように咲いています。レンギョ生垣にしたのですが、枯れたのが多く、この一箇所しか咲かなくなりました。ユキヤナギ_ブロック塀の内側に大勢咲いています。以下は数日前から咲いていたり、少し開花していたりした花でした。白木蓮幹を根元近くでカットしてしまったので花の咲き具合が少なめですが、しおれ始めたのもあって、記録しておきたかったので一輪撮影しました。ボケ赤い花を沢山つけています。豪勢に咲いています。菫車庫の入り口に近い道路脇に自然の菫が咲いています。郊外に近い場所ですので、種が風にあおられて飛んできて、此処に生えたのでしょう。 すっかり春らしくなって、花の撮影もしたくなったので、実行しました。多面体上工作を主に行っていますので、植物撮影は控えていましたが、休業も余りはなわだしいので、ブログ投稿も、こんな形勢になりました。
Mar 20, 2013
コメント(0)
-
膝痛に悩み、その特集の「わかさ」(月刊雑誌)を買う_クリスマスローズも見る
昨日の新聞に「(膝痛特集)本日発売」とあったので、榛名町の文真堂書店にバイクで行った。 図書カードが使用できたので、雑誌のほかにも、上毛新聞社発行の本二冊を購入した。「群馬の山100選」と「群馬の県境を歩く」後者は、最近出たばかりで、歩くことが出来なくなった自分を励ますつもりで、購入した。せいぜい、読むことで登山したつもりになろうと考えたのでした。 書店を出ると、その足で国道406号の南側の丘に登った。この界隈は梅ノ木が多い地域であるので観梅を楽しみながら帰宅するつもりだった。 安中市への境の峠に近いところで、左折したら「クリスマスローズガーデン」に出た。ここは、私が榛名山を撮影するときに来る絶景の望める好適地なのです。カメラが無いのに此処へ来たのは、その南側に有るガーデンハウスでコーヒータイムをしようと思ってきたのでした。 せっかくクリスマスガーデンに着たので、その花を観賞してゆこうと、傾斜の有るガーデンに上ったが、膝が痛くて歩行が大変困難だった。痛む右膝を右手で支えながら、攀じ登ったのだった。園内はジグザグに山道が作られていて、その両側にクリスマスローズが一面に咲いていた。その間に、赤い菫が咲いていた。と、私は思ったが、ガーデンの主人にもらったパンフレットで、それはシクラメンの一種である花と知った。 コーヒーハウスの中は、ドライフラワーの束が部屋中に、天井からと壁一面と、吊るされてあった。ウッドハウスで素敵なインテリアだなと思った。この日は、コーヒーハウスの中には私一人しか客はいなかった。 隣には大きな温室が有って、クリスマスローズ(白と黄色が多かった)の鉢植えが置かれた台一面に載っていた。全て値札がついていたので、覗いてみると、殆どが10000円だった。クリスマスローズって、こんなに高いのかと驚いた。帰宅して、インターネット検索して調べてみると、いろいろな色の種類があって、販売しているページを見ても、まちまちだったが1万円以上もするのは余り無かった。そのハウスに有った花は数年かけて作られたものであるから、あのように高額な値段になるのだと考えて納得した。 デジカメを持参するのを忘れたので、風景画像が撮れなかったのを残念に思っています。
Mar 19, 2013
コメント(1)
-

サンシュの花が満開です
少林山の裏山に「鼻高展望の丘」と言う大きな花園があります。その西側の牧場の入り口近く、南斜面一帯に何十本かの、いや、百本以上有るかサンシュの樹林帯があります。其処が今満開です。全部カメラに入れることが不可能なので一部を載せます。枝の間から浅間山が見えます。暖かくなって雪も大分融けたようです。向こうに見える山は榛名山です。三角に見えるのが相馬山です。 この展望花の丘は文字通り、妙義、榛名、赤城、子持ち、武尊(上州ほたか)さらに遠くは浅間山が展望できます。 春とは言え、未だ風が冷たく頬に当たります。バイクで昇りましたが、冬のジャンバーを着て行ったので、頬以外は冷たさから逃れました。膝の痛みがあって、歩き回って撮影するのは困難でした。 家に閉じこもってばかりいたのでスランプになっていたが、バイクで山道を走行してきたので気が晴れました。
Mar 16, 2013
コメント(1)
-
体罰の思い出
体罰の思い出世間では体罰の問題で騒がれています。私は現在の小学校が国民学校といわれた次代に育ったものですから体罰は日常茶飯事に行われていたように記憶しています。 その小学校時代の体罰を思い出したので、書き留めてみます。まず、小学校の一年生のとき、授業に飽きたので窓の外を見るという余所見をしたので、担任の女教師に耳を引っ張られて、「廊下に出て行きなさい」といわれたが、反発して出て行かなかったが、そのとき引っ張られた耳が大変痛かったのを思い出します。耳が千切れてしまうのではないかと思ったほどでした。 次が、三年生のとき、これも女教師に頬を叩かれた思い出です。このときはなぜ叩かれたたかは全く思い出せません。そのときの気持ちは「なぜ叩かれたのだろう?」先生には口答えは絶対にできない時代でしたから、頬を平手で打たれても、黙ってそれを受けたままでした。覚えているのは、冬のことで、その先生の手には包帯が巻かれていました。しもやけか何かで手を傷めていたのだろうと思います。学芸会の稽古をしていたときのことで、数人の児童が一緒にいました。その中で、何か私が先生の癇に障ったことを言ったのだったかと思います。それがいけないというのでしょう。えらい剣幕で叩かれたのです。しかし、包帯を巻いた手でしたから、痛かったということは覚えていません。でも、間違いなく体罰だったのです。 次は、小学校四年生のとき、数学の授業をやっていて、先生の話に飽きて余所見をしたら、授業で使っていた教師用の大きな木板で作られた三角定規の角で頭をこつんと叩かれた。木の角であったのでこの時は非常に痛かったが傷はできなかったので、それほどひどく力は入っていなかったのでしょう。この教師は男の先生でした。この教師は時々生徒を教壇の脇に立たせて平手打ちで生徒の頬を叩いていた。こんなことが平気で行われた軍国時代だったのです。小学校五年六年は優等生で、先生にほめられたことはあっても罰を受けたことは一度もありませんでした。 中学校になってからの思い出に、クラスの女生徒数人を男生徒数人で、数人といっても少人数のクラスの殆どで全員に近い人数で、「生意気な女だ、殴っちゃおう!}とクラスのボスが、クラスの男生徒にけしかけて、その数人の女生徒を家庭科教室に誘いこんで、男生徒が次々と一人づつ、その三人の女生徒に、たぶん胴体などをこぶしで叩いたのであろうと覚えています。私は、ボスの脅かしが怖かったので一緒にその部屋に行ったが、殴ることはいけないと考えていたので、殴ることはしなかった。 このことが教師に発覚されて、その家庭科の教室に、男子生徒全員が呼ばれて、一人づつ、その教師に平手で頬を叩かれた。私は「女生徒を殴らなかった」とその教師に伝えたので、平手打ちはまぬかれた。その後で裏切り者とボスに殴られるのを覚悟していたが、ボスには殴られなかった。 悪いことはできないもので、そのボスもボスの取り巻きの数人はすでにこの世にはいない。いま考えるとそのボスたちに会いたいと思っても会うことができないのが残念です。体罰はよくないことかもしれませんが、体罰が日常茶飯事に行われていた時代の懐かしい思い出ばかりです。
Mar 6, 2013
コメント(0)
-

自販機缶底のドット文字
自販機から出てくる缶の裏に書かれている文字は点の連なりで読めるようになっているが、このドット数はいくつかを調べてみた。 先ず、カメラで大きく写した。 上の画像は二つの缶の底を写した物で、ドット数は縦が7個、横が5個であることが分かった。 これを印字する印刷機のピン数は5×7=35 35本である。 1 を打つにも、只縦に一本で無く、上の横に1個、下の両脇に1個づつ、打ってある。点を打つにも、1個のドットで無く、左下に2×2で4ピンを使って打ってある。スラッシュも右上から左下に、5個のピンドットで打たれてある。 文字が35個のピンで、その中のいくつかを使って、点の連なりで書かれてあるのが面白い。 初期のパソコン用の印刷機が、これと同じタイプのものであったのと全く同じ印刷機であったのを思い出す。値段の高額のパソコンが買えなかったので、NEC製の「パピコン」と称して販売されたのを一式30万円で買ったのを思い出すが、そのときの印刷機は、全くこれと同じ物であった。漢字は書けなくて、英数字しか印刷できなかった。
Feb 25, 2013
コメント(1)
-

正6面体を特定の条件で膨らませると凧形24面体に成るという詳しい図説
左図は正6面体のひとつの面の輪郭を緑線で表している。右図のピンク線は凧形24面体のひとつの面を表している。この凧形24面体はこの輪郭で示したブロックの面が6個で構成されていると考えて、正6面体から凧形24面体が膨らんでできているというのを理解するための図です。 右図の緑線は左図の緑線と同じ大きさです。 この緑線が膨らんでピンク線と変化したとき、正6面体が凧形24面体になると理解するのです。逆も真なり右の図から左の図になるように置き換えることもできます。凧形の四辺形が四面でひとつのブロックとなって、それが6面でこの凧形24面体が構成されているので、その各ブロックをピンクの線から緑の線まで削り取れば立方体が作れます。 削り取るときの注意は、正方形の角(かど、凧形24面体のこのブロックの頂点)が同一平面であることに注意しなければなりません。六つのブロックを同じように削り取れば、その結果できた立体は正6面体(立方体)に成ります。 こんなことが考察できるのが多面体の不思議さと面白さです。難しい理論なしにトポロジーは大変面白い数学なのです。
Feb 15, 2013
コメント(0)
-

ネジ頭溝つくり
ネジ頭の溝つくりマイナスネジの溝の中央に突起があって、普通のマイナスねじ回し(ドライバ)ではネジを回せなかったのを、鉄きりノコギリでその中央の突起物を切り落とした。 最初はのこぎりの目立てようの鑢で磨耗させようと努力したがうまく取れないので、鉄きりノコギリにきりかえて作業を続けたら、マイナスねじ回しでねじれるように溝ができた。 ネジの仕上げはしてないので荒っぽいが、十分これで間に合う。ようやく元の位置にネジが収まるようになった。 以前、写真撮影したままで放置したあったのを、家電器具に収めようと考えて、作業を終わらせた。 やはり、慣れたマイナスねじのほうがドライバ操作が楽だった。マイナスねじの凹んだ中央に突起がある螺子なんてなじみがなくて、修理にてこずらされる。関連ページNov 10, 2012 マイナスでも無いプラスでも無いネジ頭_新しいドライバー造り (1)
Feb 14, 2013
コメント(2)
-

凧形24面体は正八面体を膨らませた立体でもあるという発見
正三角形の辺の長さは8.6cmこの大きさの正八面体を作って、凧形24面体と並べて写真を撮る。前頁の図説と同じように考えれば、この膨らませられた多面体の構造が理解できる。まったく不思議な多面体である。
Feb 13, 2013
コメント(0)
-

立方体を膨らませて凧形24面体が作られたという発想
凧形24面体の構成で新しい発見をした。それは、立方体を膨らませてこのような形ができたといことだった。そのことを模型で図説するため、凧形24面体の正六面体構成の頂点間6.9cmと同じ大きさの立方体を作って並べて写真を撮った。 下図がその写真です。 左の立方体の12個の辺の中点を、それぞれ同じ距離だけ外側に引き伸ばし、正方形の中点は同じ大きさの高さだけ外側に引き上げた立体が、右側の凧形24面体であると発見した。 まったく不思議な立体である。
Feb 13, 2013
コメント(0)
全1730件 (1730件中 1-50件目)











