60ばーばの手習い帳

　中１で登場する一次方程式ですが、基礎は既に小学校算数に出てきています。小６で習う文字の式と、ステップを踏んで未知の数を求める文章題が、数学の方程式を解く過程につながっていきます。

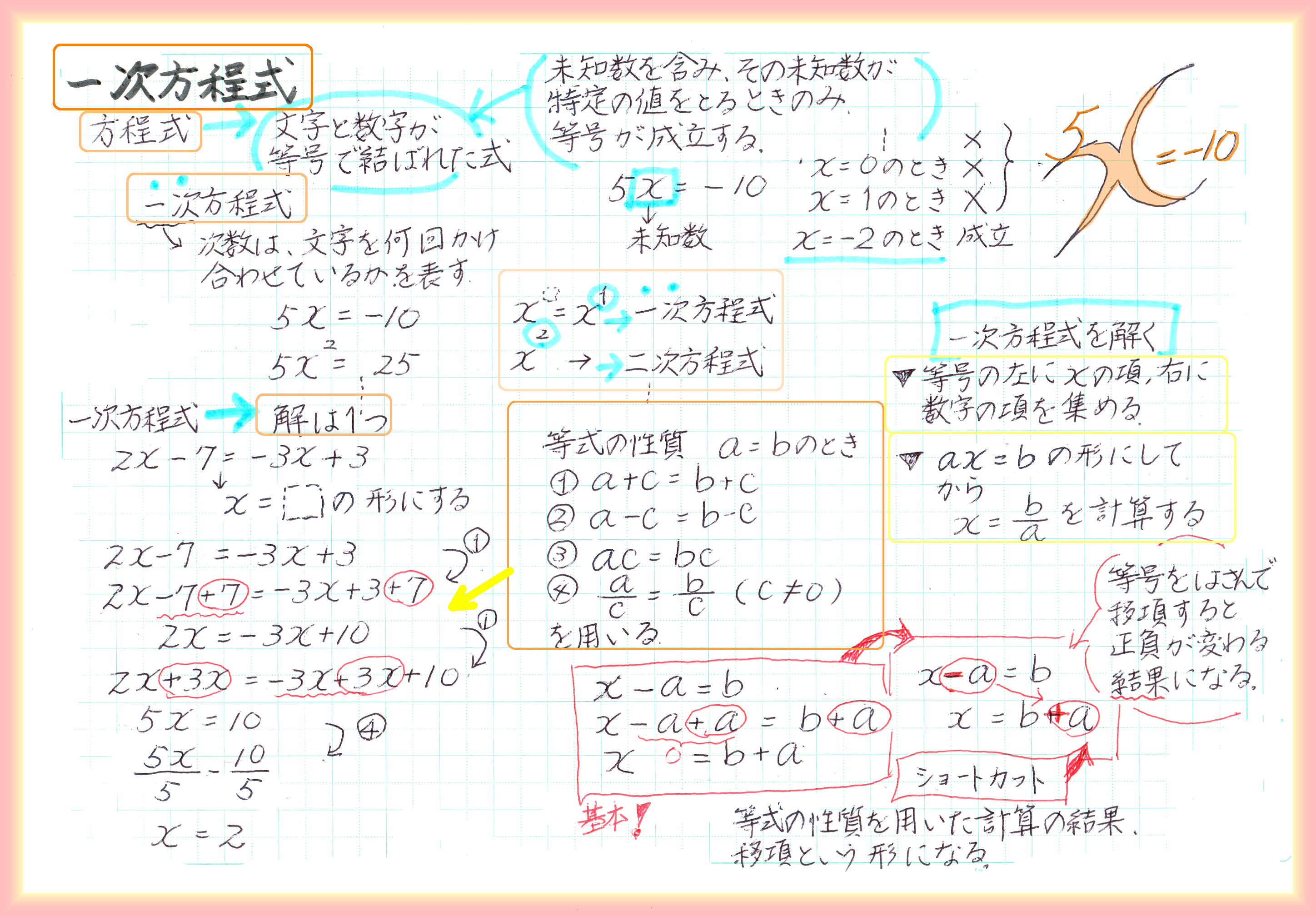
　一次方程式を解く時「移項すると足し算と引き算は符号が変わる」と覚えます。なぜ等号を越えると符号が変わるのでしょう。
　計算の過程で、等式の両辺に同じ数を足しても（同じ数を引いても）等号は成り立つという性質を使って、定数項を右辺に集めます。その計算の結果を見ると、まるで等号を越えるときに符号が変わるように見えるわけです。
　それから、両辺を同じ数で割っても（同じ数を掛けても）等号が成り立つ性質を使って未知数の係数を１にします。



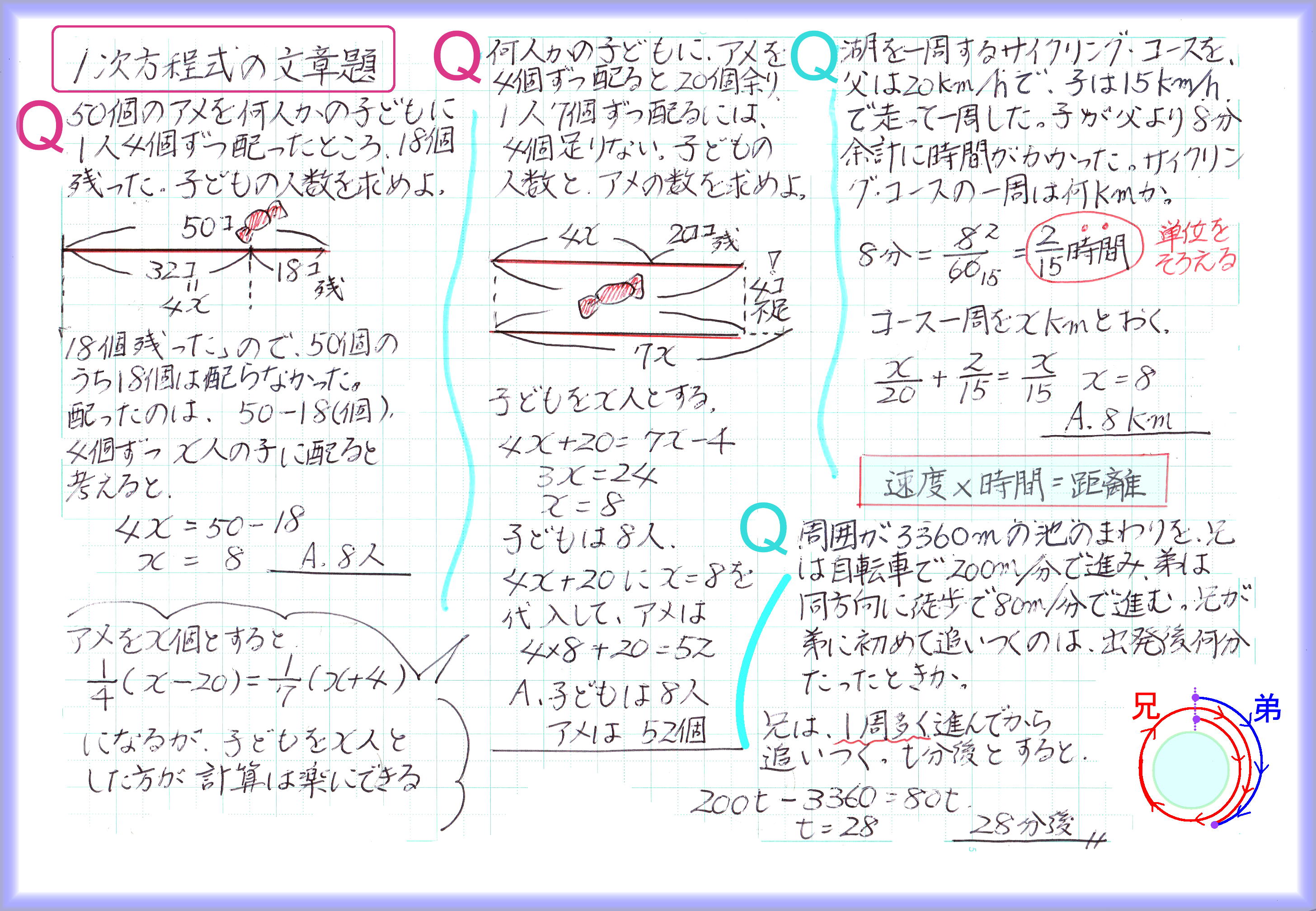
　わたしは、速さが「時速」時間が「分」という単位の違いを換算せず、沈没しました。６０分＝１時間なので、５分だったら１/１２時間、１０分だったら１/６時間に直して時速と合わせて計算しなければいけませんでした。
　時間と速度と距離の問題は小学校算数でも難問の１つだそうです。理解するには、いろいろな問題を解いてみる必要があります。


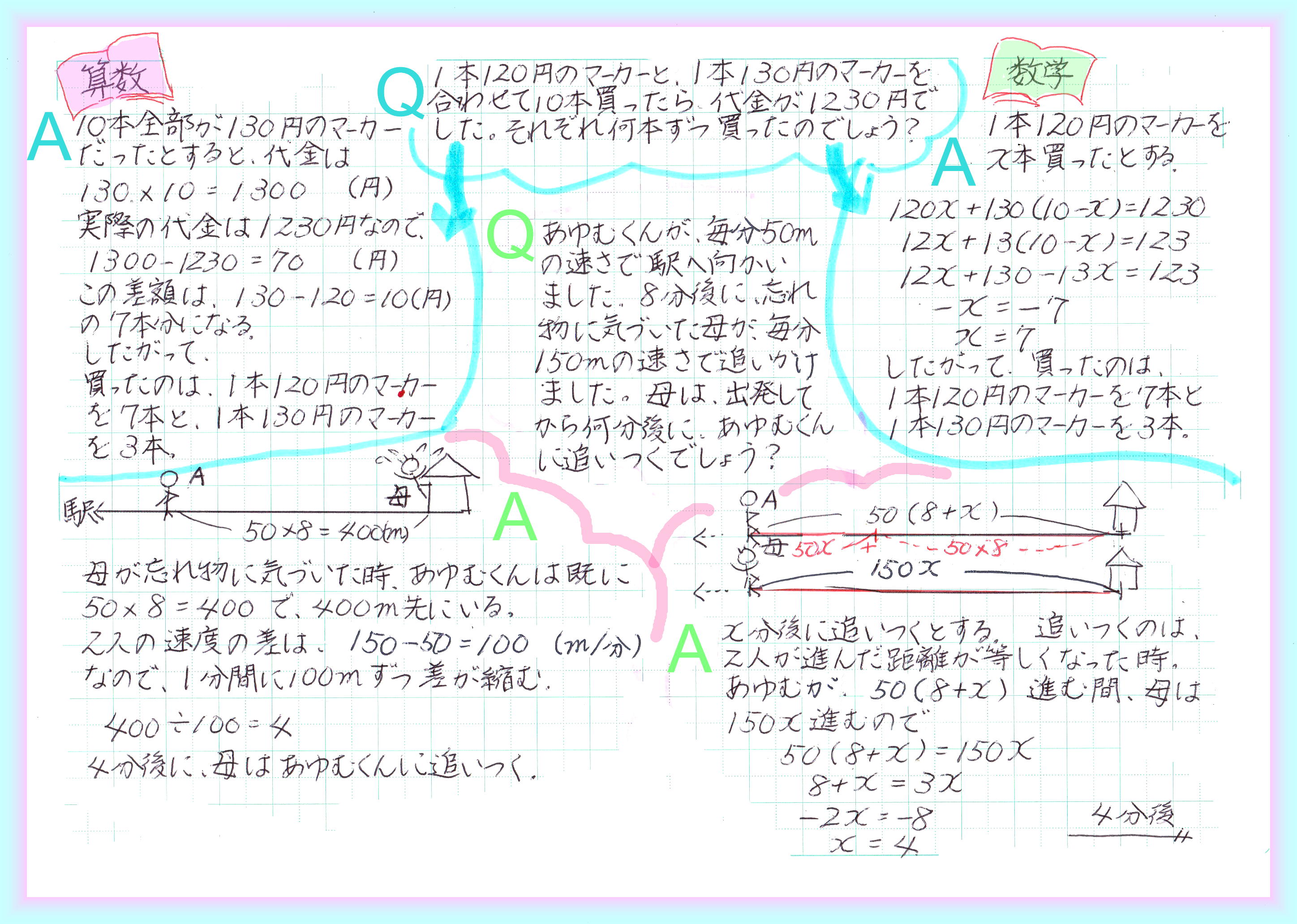
　中学校に上がると、未知数をｘに置き換えて一次方程式を立てて解く問題も、小学校では、文字を使わない式を立てて考えるほうが普通の場合があります。

　例えば「合わせて３匹の鶴と亀がいます。足が合わせて１０本のとき、鶴と亀はそれぞれ何匹でしょう」という問題に対して、全部が鶴だったら、または亀だったらと仮定して足の数の差から答を導きます。
　どうせ方程式を習えばもっと簡単に解けるのだから、苦労して考えるのは無駄なようですが、この工夫して式を立てる力がないと、数学でも壁にぶつかってしまいます。

　方程式そのものは、解き方のルールを覚えてしまえば解けますが（２次、３次方程式にも解の公式が存在します）本当に難しいのは、どんな式を立てたらよいかをみつけることです。
​